אחת הפרשיות המעניינות בתולדות האסטרונומיה הייתה התפתחות ההבנה שלנו מהו גודל מערכת השמש. בתחילה, ראה האדם את היקום כולו כקטן למדי. רק לאחר מותו של ניוטון בשנת 1727 ניתן היה להעריך את הגודל של מסלולי כדור הארץ והפלנטות, הנראות בעין בלתי מצוידת. אפילו היום עדיין מעדכנים את מבנה מערכת השמש בעקבות תובנות חדשות לגבי התפלגות הגופים הקפואים בשולי מערכת השמש. למרות שלקח אלפי שנים למפות את מערכת השמש, המיפוי עדין עובר כל הזמן עדכונים שוטפים.
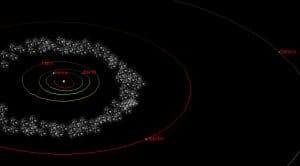
באדיבות Teach Astronomy
לפני התחלת מיפוי מערכת השמש, מתמטיקאים ניסו להשתמש בטריגונומטריה כדי למצוא את המרחקים לירח ואפילו לשמש. המדידות המוקדמות הוגבלו בשל היעדר ציוד מדויק, אך מדענים מוקדמים גילו נחישות בנסותם להסתייע בתצפיות כדי להגיע לתשובות. לדוגמה, המדידות שביצע אריסטארכוס מסמוס (310 לפני הספירה – 230 לפני הספירה) של מיקום השמש והירח, כאשר הירח נמצא ברבע הראשון (חצי מואר), אפשרו לו להשתמש בטריגונומטריה כדי להעריך את היחס בין המרחקים לשני הגופים האלו. ההערכה הגסה שלו לפיה המרחק לשמש שווה 1,200 רדיוס כדור הארץ (כ- 8 מיליון ק"מ), הייתה רחוקה מהערך הידוע כיום של 150 מיליון ק"מ, אך הייתה טובה למדי בהתחשב בחסרונם של כלי תצפית מודרניים כמו טלסקופים. התוצאות שלו היו שגויות מאוד, אך הן היו הבסיס להתפתחותן של שיטות יעילות יותר.
ארטוסטנס (Eratosthenes) ביצע את התקדמות משמעותית ראשונה כאשר הצליח למדוד את גודל הפלנטה עליה אנו חיים. הוא ביצע זאת באמצעות יישום מרהיב של הנמקה גיאומטרית, סביב 200 לפנה"ס. ארטוסטנס היה חוקר וספרן בספריה הגדולה באלכסנדריה, במצרים, שם אוחסנו ספרים המכילים חלק גדול מהידע של העולם העתיק. הוא השלים קטלוג של 675 הכוכבים הבהירים ביותר, אך ההישג המפורסם ביותר שלו היה מדידת גודל כדור הארץ.
ארטוסטנס טען כי השמש ביום הארוך בשנה (21 ביוני), נמצאת במצב זניט ליד אסואן, הוא ציין כי באותו תאריך באלכסנדריה, כיוון השמש לא היה אנכי אלא בערך °7, או 1/50 מעיגול. ארטוסטנס הבין שהבדל זה נובע מפני השטח העגולים של כדור הארץ וכי המרחק הזוויתי בין אלכסנדריה לאסואן חייב להיות 1/50 מהיקף כדור הארץ. במדידת המרחק ביחידה עתיקה שנקראה סטאדיה והכפלה ב- 50, הוא קיבל הערכה של היקף כדור הארץ שהיה בין 1% ל- 10% מהתשובה הנכונה. בתקופה בה אנשים מעטים נסעו יותר מחמישים ק"מ בחייהם, וכאשר הזמן עד לההקפה הראשונה של כדור הארץ היה גדול יותר מ- 1000 שנים, היוונים המשכילים ביותר ידעו את גודל הפלנטה עליה הם חיו! (וידעו כי כדור הארץ היה עגול.)
באדיבות Teach Astronomy
במשך מאות השנים הבאות אנשים ניסו לקבוע את סדר פלנטות ולבנות מודלים מתמטיים שינבאו את מיקומן. הם הבינו נכונה כי פלנטות שנעות לאט יותר על פני השמים, כמו שבתאי וצדק, הן רחוקות יותר מפלנטות שנעות במהירות גדולה יותר, כמו מרקורי ונוגה. כמו כן, הובן כי הכוכבים רחוקים יותר מהפלנטות. מה שלא הובן היה המרחק אל הכוכבים. ההנחה הייתה שהכוכבים קרובים למדי, רק קצת מעבר למסלולו של צדק. ההנחה הזו, שכוכבים קרובים, היא שהובילה לאמונה מוטעית, שכדור הארץ נמצא במרכז מערכת השמש. כאשר השמש נמצאת במרכז, מראה הכוכבים הקרובים מכדור הארץ היה משתנה, וניתן היה לצפות בתנועת פראלקסה שלהם בזמן שכדור הארץ סובב סביב השמש. אך בפועל לא ניתן היה להבחין בפראלקסה. לתצפיות שביצע גלילאו ב- 1609, שבהן אישר את התיאוריה של קופרניקוס, לפיה השמש נמצאת במרכז מערכת השמש, הייתה משמעות דרמתית. פירושן היה שעלינו להזיז את הכוכבים למרחק גדול הרבה יותר. המרחק המינימלי עד לכוכבים הפך להיות המרחק הנדרש כך שהכוכבים לא יזוזו, כאשר צופים בהם מכדור הארץ, המקיף את השמש. תובנה זו גרמה להכפלת גודל היקום הידוע לפחות בשני סדרי גודל. אמנם הדבר קירב אותנו במעט להבנת מיקומם של הכוכבים, אך עדיין לא הצלחנו להבין מהם המרחקים לפלנטות.
במקביל לגלילאו עמל יוהנס קפלר על סידור מחדש של מערכת השמש, תוך ניסיון להגדיר את המתמטיקה שמאחורי תנועות פלנטות. באמצעות חוקי קפלר, אסטרונומים יכולים לקבוע את המרחקים היחסיים של כל פלנטות מהשמש. חישוב זה נעשה בהתבסס על השלישי של קפלר הקובע את הקשר בין זמן ההקפה לבין המרחק מהשמש. אולם החוק השלישי אינו מאפשר קבלה של מרחקי הפלנטות ביחידות כמו קילומטרים. בשלב זה כל שניתן היה לעשות, היה להשוות את המרחק בין כדור הארץ לשמש, אל שאר המרחקים של הפלנטות.
אסטרונומים מגדירים את המרחק הממוצע מכדור הארץ לשמש כיחידה אסטרונומית אחת או AU. מרחקים לגופים אחרים במערכת שמש אחרים מבוטאים בכפולות של AU. זוהי יחידת המדידה השימושית ביותר באסטרונומיה של מערכת השמש, פרט למערכת המטרית. באמצעות מרחק זה כאמת מידה, ניתן לחשב את המרחקים לכל שאר פלנטות, בעזרת זמן המחזור והחוק השלישי של קפלר. לכן, האתגר העיקרי שנותר בקביעת קנה המידה של מערכת השמש היה מדידה מדויקת של המרחק המוחלט מכדור הארץ לשמש (או מכדור הארץ לפלנטות אחרות, שניתן לבטאם בעזרת מרחק ארץ-שמש).
לאחר המצאת הטלסקופ ניתן היה למדוד את גודל הזווית של כוכב לכת. טלסקופ בגודל צנוע מציג את גודלו הזוויתי של מאדים כ- 30 שניות קשת, במצב הקרוב ביותר לכדור הארץ. אם נניח שמאדים בעל גודל השווה לכדור הארץ, באמצעות משוואת הזוויות הקטנות נקבל את המרחק,
D = 206,265 × (d / a) = 80 million kilometers
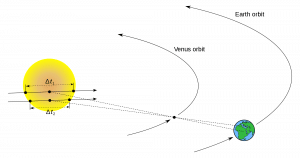
מרחק זה מתבסס על ניחוש מוחלט, שמאדים וכדור הארץ הם בעלי אותו גודל, כך שברור שזה איננו מספר אמין. אם נסתייע בקוטר כדור הארץ כבסיס הפראלקסה, ניתן להשתמש בזווית פראלקסה גם למדידת המרחק מכדור הארץ למאדים. בשיטה זו נעשה שימוש במשולש חד זווית וארוך מאוד – מרחקו של מאדים גדול אלפי פעמים בהשוואה לגודל כדור הארץ. לכן, זווית הפראלקסה קטנה מאד, וקשה למדוד אותה. נוגה מתאימה יותר לצורך קביעת AU, מכיוון שפעמיים בכל 110 שנים צופה על כדור הארץ רואה אותה עוברת על פני השמש. באסטרונומיה תופעה זו נקראת – מעבר (transit). השמש מספקת תפאורה מושלמת לצפייה בדיסק הקטן והכהה של נוגה. בעזרת תצפיות משני אתרים מרוחקים על פני כדור הארץ, ניתן למדוד את זווית הפראלקסה, ולחשב את המרחק מכדור הארץ לנוגה. עם המרחק הזה, בתוספת מדידה של המרחקים היחסיים בין כדור הארץ, הנוגה והשמש, אפשר לחשב את המרחק הכולל מכדור הארץ לשמש. המרחקים היחסיים בין מסלוליה של נוגה וכדור הארץ היו ידועים מאז ימיו של ניקולס קופרניקוס, שחישב אותם באמצע המאה ה -16.
באדיבות Teach Astronomy
ישנם שני סיבוכים בשימוש בשיטת הפראלקסה למדידת המרחק לנוגה. ראשית, כדור הארץ מסתובב. יש לבצע את התצפיות בדיוק באותה שעה, ושגיאה במדידת זמן בפלנטה מסתובבת מביאה לשגיאה במרחק, וכך לשגיאה במדידת הפראלקסה. ההקפדה על מדידת הזמן חשובה גם בניווט. ניתן להשתמש בזווית הכוכבים לניווט בשעות הלילה (למשל, שימוש בכוכב הצפון). אך נדרש שמירת זמן מדויקת לקביעת קו האורך. כדור הארץ מסתובב במהירות של 15 מעלות לשעה, כך ששעון שנמצא כבוי רק כחצי שעה לאחר הפלגה בים היה גורם לשגיאת ניווט של:
7.5° / 360°=0.021=2.1%
בקו המשווה זוהי שגיאה של כ- 1000 ק"מ! שעונים גרועים היו הסיבה לניווט גרוע בספינות במאה ה-17 ועוד לפני כן. גם במסע המפורסם של כריסטופר קולומבוס נוצרה בעיית ניווט שכזו. הבעיה זו נפתרה באמצע המאה ה -18 כאשר ממשלת בריטניה הבינה כי שעון מדויק הוא המפתח לניווט טוב בים. בעקבות תחרות, שבה הוצע פרס של 20,000 ליש"ט, ג'ון האריסון ייצר שעון מדויק בעל שגיאה של 5 שניות ב- 80 יום, שהוא מכשיר זמן יוצא מן הכלל בכל עידן.
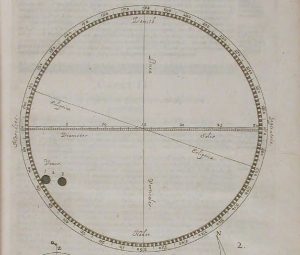
בעיה נוספת בהתבוננות במעבר של נוגה הייתה הצורך במזל, מכיוון שזוגות של מעברי נוגה מתרחשים רק פעמיים בכל 110 שנים. לפני שמת יוהנס קפלר בשנת 1630, הוא חזה שמעבר נוגה הבא יתרחש בשנת 1631 – אך למרבה הצער, איש לא צפה בו משום שהמעבר התרחש במהלך הלילה עבור אסטרונומים אירופאים. אסטרונום ואיש דת צעיר בשם ג'רמיה הורוקס הצליח לחזות ולצפות במעבר הבא בשנת 1639. תיעד הורוקס חלק מהאירוע עד שקיעת החמה. באמצעות הגדלים היחסיים של הדיסק של נוגה ושל הדיסק של השמש, חישב הורוקס את מרחק כדור הארץ-שמש כ- 14,700 רדיוס כדור הארץ (98 מיליון ק"מ). ערך שהיה טוב בהרבה, וגדול בהרבה מכל מדידה קודמת.

באדיבות Teach Astronomy
בידיעה שתצפיות טובות על מעבר נוגה יקבעו את גודל מערכת השמש, אסטרונומים נאלצו להמתין יותר ממאה שנים עד זוג המעברים הבא בשנת 1761 ו -1769. אדמונד האלי חזה את המעברים הללו בשנת 1716. מודע לכך שהוא לא יזכה לראותם, הוא דחק באסטרונומים עתידיים לערוך תצפיות זהירות. הפצרותיו הצליחו, ומסעות מדעיים רבים יצאו לרחבי העולם כדי לבצע את התצפיות הנחוצות בקווי הרוחב המרוחקים זה מזה. כבר אז סבלו ההרפתקנים ממסעות ים מפרכים, רק כדי שיצליחו להתמודד עם שודדי ים, טייפונים או סופות גשמים. בשנת 1769 ערך קפטן ג'יימס קוק מסע מפורסם כדי לצפות במעבר נוגה בטהיטי. תצפיותיו, בשילוב עם אלה של אסטרונומים אחרים מרחבי העולם, קבעו את המרחק מכדור הארץ לשמש ברמת דיוק של 10% מערכו המודרני כ- 150 מיליון ק"מ.
מדידות המעבר הללו לא רק קבעו את קנה המידה הנכון של מערכת השמש, אלא גם היוו גם דוגמא חשובה וראשונה בהיקפה למאמץ בינלאומי של שיתוף פעולה מוצלח בין מדענים. המעבר האחרון של נוגה בשנת 2004 סיפק הזדמנות לאסטרונומים חובבים להשתתף בניסוי שיתופי דומה על ידי העתקת המדידות ההיסטוריות הללו בעצמן. המעבר האחרון של נוגה התרחש בשנת 2012 – אני מקווה שצפיתם בו מכיוון שאולי לא תהיו בחיים בשביל לצפות במעבר הבא!
מדידת המרחקים לפלנטות בוצעה מאז מלחמת העולם השנייה. במדידות רבות מסתייעים המדענים מכ"ם (מגלה כיוון מרחק) כדי להגיע לתוצאות מדויקות מאד, בעזרת נקבעים הגדלים והאקסצנטריות של מסלולי הפלנטות והירחים במערכת השמש שלנו.
Author: Chris Impey

