
באדיבות וויקיפדיה
הקוסמולוגיה המודרנית החלה עם אלברט איינשטיין. ראשית, תורת היחסות הפרטית שלו הראתה כי הזמן והמרחב הם גמישים ולא מתוארים כראוי על ידי הצעדים הליניאריים והנוקשים שהציע ניוטון. הניסוי מראה לנו כי מהירות האור היא בעלת ערך קבוע, ללא קשר לתנועת הצופה. ישנן שלוש תוצאות מוזרות הנובעות מהעובדה שאיננו יכולים למדוד את המהירות שלנו ביחס לקרן אור: (1) הזמן מאט עבור גוף הנע ביחס אלינו. (2) גוף נע מתכווץ בכיוון תנועתו. (3) מסה של גוף נע במהירות גבוהה גדילה, כאשר אנרגית התנועה מומרת למסה באמצעות הקשר המפורסם E = mc2. תופעות אלו אינן קיימות בעולם היומיומי, שבו גופים נעים לאט בהשוואה למהירות האור.
תורת היחסות הפרטית עוסקת בגופים בתנועה יחסית קבועה. לעומת זאת, תורת היחסות הכללית עוסקת בגופים הנעים בתנועה שאינה קבועה. איינשטיין הוביל את תורת היחסות הכללית בעקבות מחשבות על צירופי מקרים בפיזיקה. המסה הכבידתית של גוף – תגובתו לכוח כבידה – זהה למסה האינרציאלית שלו – ההתנגדות שהיא מציגה לשינוי בתנועה. במבט ראשון נראה כי אלה צורות שונות מאוד של מסה. תארו לעצמכם חתיכת ברזל גדולה וחלקה הנמצאת במנוחה על משטח חלק וקפוא. המסה הכבידתית מכתיבה את הכוח שבו לוחץ הברזל על הקרח. המסה אינרציאלית מייצגת את התנגדות של ברזל לשינוי במהירות, כאשר כוח מנסה להאיץ או להאט אותו. למסה אינרציאלית אין שום קשר עם כוח הכבידה, שכן התנועה על הקרח היא אופקית וכוח הכבידה פועל אנכית. אף על פי כן, המסה האינרציאלית ומסת הכבידה נמדדים ברמה דיוק גבוהה: כך שהניסויים המודרניים מוצאים כי ההבדל בין שתי המסות הוא פחות מ- 1 חלקי 1015. איינשטיין האמין כי צירוף מקרים זה מצביע על המפתח להבנת כוח הכבידה.
אנלוגיה תציג עד כמה קשה להבחין בין תנועה הנגרמת על ידי כוח הכבידה והתנועה שנגרמת על ידי כוח אחר. נניח שאתה לכוד במעלית ללא חלונות. איינשטיין הראה כי אין דרך להבחין בין תנועה של גופים במעלית מואצת לבין תנועתו של גוף הנוח על פני כדור הארץ או נע במעלית המואצת בחלל רחוק בשיעור של 9.8m/s2. בכל מקרה תשקול אותו דבר. הוא גם הבין כי אין דרך להבחין בין תנועה של גופים במעלית או גופים המרחפים בחופשיות בחלל. במעלית מואצת קיימת נפילה חופשית בדומה לזו המוכרת לנו מפני כדור הארץ, בתאוצה של 9.8m/s2. בשני המקרים אתם תהיו חסרי משקל. בקיצור, אין הבדל בין ההאצה שנגרמת על ידי כוח הכבידה והאצה בשל כוח אחר.
באדיבות וויקיפדיה
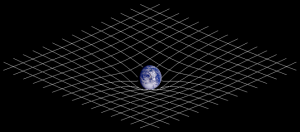
כוח הכבידה הוא אם כן דרך נוחה לתאר כיצד נוכחות המסה גורמת לגוף לשנות את תנועתו. איינשטיין יצר "הכללה" של תורת היחסות הפרטית בכך שהראה כיצד יכול כוח הכבידה לעוות את הזמן ואת המרחב. תורת היחסות הכללית מחליפה את כוח הכבידה של ניוטון בגיאומטריה של החלל עצמו. הרעיון הניוטוני המוכר של מסות המוצבות במרחב חלק ואחיד מוחלף ברעיון בלתי-אינטואיטיבי של המרחב המעוות בהשפעתן של מסות שהוא מכיל. החומר מעוות את החלל, ואור וחלקיקים עוקבים אחר הנתיבים המתעוותים שמכתיבה עקמומיות החלל.

באדיבות וויקיפדיה
בשנת 1917, החליט איינשטיין ליישם את המשוואות של תורת היחסות הכללית על היקום כולו. הוא הניח כי היקום סטטי, משום שהאסטרונומים האמינו באותה עת שהיקום מכיל רק את שביל החלב העצום, כשכוכבים מסתובבים בו. (למרבה האירוניה, האסטרונום, וסטו סליפר, שכבר אסף ספקטרום של גלקסיות, חשף את התפשטותן של הגלקסיות, והפריך את המודל הסטטי.) לא משנה באיזו דרך איינשטיין פתר את המשוואות, אך הן הצביעו באופן עקבי על כך שהיקום דינאמי, כלומר מתרחב או מתכווץ. כדי לאלץ פתרון סטטי למשוואותיו, הוסיף איינשטיין קבוע שרירותי. איינשטיין הודה מאוחר יותר כי תוספת זו הייתה "הטעות הגדולה ביותר בחיי". בשלה, החמיץ איינשטיין את ההזדמנות לחזות את התפשטות היקום עשר שנים לפני שהאבל גילה זאת בדרך תצפיתית.
בשנות העשרים, המתמטיקאי הרוסי אלכסנדר פרידמן והמתמטיקאי הבלגי ז'ורז' למטר פתרו באופן בלתי תלוי את המשוואות של תורת היחסות הכללית והראו מתמטית שהיקום אכן מתפשט. לאחר מכן, בעקבות גילויו היחס של האבל בין המרחק להסחה לאדום, התברר כי מה שנראה במקור כמודל תיאורטי גרידא נתמך על ידי תצפיות. גלקסיות אינן מתרחקות זו מזו בחלל בגרסה המורחבת של אפקט דופלר. הגלקסיות מתפרקות בשל התפשטות החלל עצמו. מהירויות ההתפשטות של גלקסיה מאובחנת בעזרת היסט לאדום קוסמולוגי. אנחנו יכולים לחזור על אנלוגיה פשוטה: פני השטח של בלון שעליו מודבקים חרוזים קטנים המייצגים גלקסיות. (יש לזכור כי זהו ייצוג דו ממדי של חלל מעוקם חיובית, המתקיים בשלושה ממדים.) בדומה לבלון מתנפח, ההתנפחות שלו מגלה כמה תכונות רלוונטיות ליקום המתפשט.

באדיבות וויקיפדיה
האנלוגיה בין הבלון המתנפח לבין היקום המתפשט מדויקת בהיבט הבא: המרחק בין החרוזים, המיצגים את הגלקסיות, נגרם בשל מתיחת החומר ממנו עשוי הבלון. בתורת היחסות הכללית, החלל המתרחב, נושא עמו את הגלקסיות. מהירות ההתפשטות של החרוזים, בעקבות חוק האבל, נמצאת ביחס ישר למרחק ביניהם. אין חרוז במרכז הבלון, ואין חרוז בקצהו. למרות שהחלל מתרחב, החרוזים נשארים באותו גודל. ביקום שלנו, למרות שהגלקסיות והצבירים מתרחקים זה מזה, כוח הכבידה הפנימי שלהם מונע מהם להתרחב. אזורים אלה של מרחבים שאינם מתרחבים מתוארים היטב על ידי חוקי ניוטון: מערכת השמש אינה מתרחבת, וגם לא הבית שלך. שימו לב, כאשר הבלון מתרחב, עקמומיות החלל פוחתת: חישבו על ההבדל בין עקמומיות בלון בגודל אגרוף לבין העקמומיות של בלון בגודל של בית. אנחנו יכולים עתה להוסיף לבלון אנלוגיה של הסחה לאדום הקוסמולוגי. תארו לעצמכם שגל אור (או כל גל אלקטרומגנטי) משורטט על הבלון בזמן שאורכו קטן. כאשר הבלון מתנפח, אורך הגל גדל או שצבעו מאדים. ביקום האמיתי, אור העובר דרך מרחבים הולכים וגדילים, ואנו רואים היסט לאדום שגדל עם המרחק שעבר האור.
ליקום המתפשט יש עקמומיות בחלל. הדרך הטובה ביותר למדוד את העקמומיות היא באמצעות מדידה של סטית האור. אם האור וכל הצורות האחרות של אנרגיה אלקטרומגנטית יש מסה שקולה, שערכה נתון על ידי E = mc2, אזי האור צריך להגיב לעקמומיות החלל בדיוק כמו שחלקיקים אמורים לעשות. קרן אור החוצה מעלית שמאיצה בחלל, מוסחת במידה זעירה, מפני שבמשך הזמן שנדרש למעבר המעלית, המעלית זזה. עם זאת, איינשטיין הראה כי לא ניתן להבחין בין מצב זה לבין מצב שבו ממעלית נחה על פני כדור הארץ, האור יסטה באותה מידה. איינשטיין ניבא כי האור יסטה בשל כוח הכבידה של כדור הארץ! המסה מעקמת את החלל, וגם הקרינה וגם החלקיקים עוקבים אחר המסלולים המוכתבים על ידי עקמומיות זו.
אסטרונומים יודעים כי שטח יכול להיות מעוקם מקומית. התצפית כי אור הכוכבים סוטה ממסלולו בעבורו סמוך לקצה השמש ב- 1.8 שניות קשת (רק 0.1% מקוטר זווית של השמש!) היה אישור דרמטי לתורת היחסות הכללית. התופעה של עדשת כבידה מתרחשת משום שגלקסיה או צביר גלקסיות מעוותות את החלל וגורמות לעיוות מסלול האור מקווזאר או מגלקסיה הנמצאת ברקע. בדוגמה הקיצונית של חור שחור, החלל מעוקם עד כדי כך שהוא "מכווץ" לנקודה אחת, לכן חומר וקרינה הנלכדים באופק אירועים אינם יכולים להיחלץ ממנו.
תורת היחסות הכללית מאפשרת לחלל להתעקם באופן כללי בהשפעת כל החומר והאנרגיה שביקום. כדי להבין זאת, כדאי לחקור את ההבדל בין גיאומטריה אוקלידית לבין גיאומטריה שאינה אוקלידית. כוח המשיכה של ניוטון הסתמך על הגיאומטריה התלת-ממדית המוכרת של אוקלידס. בגיאומטריה האוקלידית, החלל שטוח ולמשטחים דו-ממדיים אין עקמומיות. סכום הזוויות במשולש אוקלידי הוא 180 מעלות, וקווים מקבילים או קרני אור מקבילות לעולם לא ייפגשו. החלל האוקלידי שטוח.

באדיבות וויקיפדיה
בסוף המאה התשעה-עשרה, מתמטיקאים בגרמניה, איטליה ורוסיה הוקסמו מסוגים שונים של גיאומטריה, השונה לחלוטין מהגיאומטריה האוקלידית ומהחוויה היומיומית. אף אחד מהמתמטיקאים האלה לא חלם שהעבודה האזוטרית שלהם תיושם במרחבי הקוסמולוגיה. שני סוגים של חלל לא אוקלידי קיימים: כדורי והיפרבולי. קיימת גיאומטריה מעוקלת חיובית, באנלוגיה שלנו היא כמו פני כדור. בגיאומטריה זו סכום הזוויות במשולש גדול מ- 180 מעלות, וקווים מקבילים או קרני אור מתכנסים, כך שמרחב כדורי זה נקרא גם מרחב "סגור". מעט פחות מוכרת היא הגיאומטריה המעוקמת שלילית, באנלוגיה המרחב מעוצב בדומה לאוכף או היפרבולה בשני ממדים. סכום הזוויות במשולש הוא פחות מ- 180 מעלות, וקווים מקבילים או קרני אור מתרחקים, כך שמרחב היפרבולי נקרא גם מרחב "פתוח".
לפניכם סיכום של שלושה סוגים של עקמומיות בחלל: אוקלידית (או שטוח), כדורית, היפרבולית:
• אוקלידית: אפס עקמומיות, נפח אינסופי, סכום זוויות המשולש =° 180, קווים מקבילים נשארים מקבילים
• כדורי: עקמומיות חיובית, נפח סופי, סכום זוויות המשולש > ° 180, קווים מקבילים מתכנסים.
• היפרבולי: עקמומיות שלילית, נפח אינסופי, סכום זוויות המשולש < ° 180, קווים מקבילים מתבדרים.
ניתן להשתמש באנלוגיה לחלל דו מימדי המעוות כי ניסיון ואינטואיציה עשויים לסייע בהבנת מצב דו מימדי, לעומת זאת המצב תלת מימדי קשה להבנה ללא טיפול מתמטי. גודל פני השטח של משטח שטוח או פתוח הוא אינסופי. נסו לדמיין את סדין שנמשך לכל עבר. (בשלושה ממדים מדובר בנפח אינסופי.) לעומת זאת, השטח של משטח סגור הוא סופי ולכן גם הנפח שלו. המשטח הדו-מימדי של כדור הארץ, למשל, הוא משטח סגור. עם זאת, כדור הארץ הוא גם חסר קצוות: יש לו שטח מסוים אבל אתה יכול לנסוע בכיוון אחד לנצח מבלי להגיע לקצה. לפי האנלוגיה, אנו יכולים לדמיין את היקום כחלל סגור, שבו הגלקסיות נמתחות בחלל לכל כיוון, אבל אין ליקום קצוות. האנלוגיה הזאת עונה על השאלה עתיקת יומין של ארצ'יטוס ושל הוגים יווניים אחרים: האם יכול היקום להיות סופי וחסר גבולות?
כיצד נוכל להוכיח שהאנלוגיה מייצגת באמת את היקום? חוויית היומיום מאפשרת לנו להעריך האם החלל מעוקם או לא. באופן דומה, ניתן להתרשם ממדבר או אוקיינוס, כוכב הלכת שאנו חיים עליו נראה שטוח. אף טכניקת מדידה מקומית לא תציג סטייה מהגיאומטריה האוקלידית. עם זאת, תצפיות ממרחק גדול אכן יאפשרו למדוד את העקמומיות של כדור הארץ. אם ניסע לאורך קו המשווה של כדור הארץ ממזרח למערב, ניתן לבצע פנייה ימינה (זווית ° 90) כך שכיוון הנסיעה יהיה לכיוון הקוטב הצפוני. בקוטב הצפוני, נבצע עוד פניה ימינה בזווית ישרה ביחס לכיוון ממנו הגענו, עתה ניסע בחזרה לכיוון קו המשווה. בקו המשווה, נבצע פנייה שלישית ימינה, ננוע שוב לאורך קו המשווה ונגיע למקום שבו החל המסע. סכום הזוויות במסע המשולש הזה הוא ° 270 – הוכחה לכך שהארץ אינה משטח שטוח! כמו כן, אם ניסע ישר לכל כיוון על פני כדור הארץ במשך זמן מספיק, בסופו של דבר נחזור לנקודה שבה התחלנו. אנחנו לא יכולים לשכפל ניסויים אלה ביקום התלת-ממדי, אבל אסטרונומים המציאו דרכים חכמות לנסות למדוד את עקמומיות החלל.
Author: Chris Impey

