מדענים מציגים את הראיות שלהם באמצעות מדידות. אנשים מציגים טענות רבות בחיי היומיום. חלקן איכותיות וחלקן כמותיות. חבר יכול לומר "המוזיקה הזאת נהדרת!" או "אתמול היה קר יותר מאשר היום", או, "יש רק ארבעה כוחות בטבע." אין דרך אמינה לכמת את הטענה הראשונה, למרות שהחבר שלך עשוי להרגיש שעמדתו נכונה. עם זאת, שתי הטענות הבאות ניתנות לכמות, ואפשר למדוד אותן במטרה לתמוך או להפריך אותן. במדע, אנחנו מנסים להתמודד רק עם טענות שניתן לכמתן. אחרת, לא תהיה לנו שום דרך להשוות בין התוצאות. מדענים משתמשים במדידות כדי להגיע לטענות מדויקות וכמותיות. המדידה חייבת לכלול שני מרכיבים: מספר ויחידה, המציינים את סוג הכמות שנמדדת. שימו לב שמספרים בלבד אינם מועילים. היחידות חייבות להיות חלק ממערכת מוגדרת היטב. ניתן לכמת את ההצהרה "אתמול היה קר" כאשר טוענים " אתמול היו 15 מעלות," אבל עדיין צריך לדעת אם המדידה הייתה בסולם צלזיוס או בסולם פרנהייט. ההצהרה "שוק המניות ירד 50 נקודות" ניתנת לכימות, אך לא ניתן להבין זאת. עליכם לדעת מה בעצם מייצגת נקודת בממוצע של דאו ג 'ונס. אסטרונומים צריכים להתמודד עם מספרים גדולים מאוד מאוד. סימון מדעי הוא קיצור שימושי לכתיבת מספרים בכל גודל רצוי (הוא נקרא לעתים קרובות כתיב חזקות או סימון מעריכי). לדוגמה, במקום לומר כי הכוכב הקרוב ביותר הוא במרחק של כ- 40,000,000,000,000 ק"מ מאתנו, ניתן לומר כי הוא 4 כפול 1013 (המעריך "13" מייצג את מספר אפסים לאחר הספרה המשמעותית "4").
מערכת היחידות במדעי הטבע היא פשוטה להפליא. כל המדידות המגוונות שאנו יכולים לבצע בעולם הפיזי – מהירות, כוח, טמפרטורה, מטען חשמלי, אנרגיה וכן הלאה – נגזרות משלוש תכונות בסיסיות בלבד: מסה, אורך וזמן. למאפיינים אלה אנו מצרפים את היחידות המוכרות במערכת המטרית: קילוגרם למדידת מסה, מטר למדידת אורך ושניות למדידת הזמן. כמעט כל סוג אחר של מדידה הוא רק שילוב של יחידות אלה. לדוגמה, השטח הוא אורך כפול אורך, התנע הוא רק מסה כפול מהירות – כלומר מסה כפול אורך חלקי הזמן. אפילו מושגים כגון אנרגיה או טמפרטורה יכולים להתבטא כשילובים של אותן שלוש תכונות בסיסיות. מערכת פשוטה של יחידות מסייעת למדענים להבין את עולמינו המסובך.
מדוע מדענים משתמשים בדרך כלל ביחידות במערכת המטרית? השיטה המטרית הוכנסה לשימוש נרחב לאחר המהפכה הצרפתית של 1789. האדריכלים של המהפכה הצרפתית רצו להפסיק את תרבות המוגדרת על ידי תמלוגים וכוח תורשתי, ולהוביל עידן של התבונה. כחלק ממערך גורף של שינויים חברתיים, הם הציגו סדרה של יחידות המבוססות על מערכת ספירה עשרונית. מערכת מטרית נועדה להחליף את המערכת האנגלית שבה נפח של גלון הוא 8 פיינט (pints), אורך של רגל היא 12 אינץ ', משקל של פאונד הוא 16 אונקיות, לירה שטרלינג היא 20 שילינג, וכן הלאה. יחידות אלה מקורן בהיסטוריה האירופית של ימי הביניים! בתקופה שבה מעט אנשים ידעו קרוא וכתוב או ביצעו פעולות החשבון, היה קל יותר לבצע מדידות באמצעות מספרים שקל לחלקם. למספרים 8, 12, 16 ו -20 יש שלושה גורמים או יותר, בעוד של 10 יש רק שני גורמים.
מערכת היחידות המטריות פשוטה הרבה יותר. לדוגמה, מטר הוא 100 ס"מ, וקילומטר הוא 1000 מטר. תומס ג'פרסון התרשם מאוד מהמערכת המטרית ודחף לקבלתה בארצות הברית. הוא היה מאוכזב מאוד אילו ידע שכמעט 230 שנה לאחר מכן, ארצו היא המחוז האחרון בעולם המתנגד לאימוץ השיטה המטרית. האירוני הוא שהחברה הטכנולוגית המתקדמת ביותר בעולם עדיין נאחזת באינצ'ים, מיילים, אקרים, גלונים, פייינטים, פאונדים ואפילו בדירוגים של כוח סוס! היחידות האנכרוניסטיות האלה אינן מאפשרות לבצע מדידות מדויקות, והתוצאה היא הפרדה עדינה אך עמוקה בין מדענים לבין כלל הציבור.
האסטרונומיה עוסקת בטמפרטורות קיצוניות החל בקור של מרחב בין-גלקטי המגיע לכדי 3 מעלות קלווין מעל האפס המוחלט ועד טמפרטורת גל ההלם של סופרנובה המגיעה לכדי מיליארד (109) מעלות קלווין. הגדלים בהם עוסקת האסטרונומיה מתחילים בגרגרי אבק קוסמיים בגודל מיקרוסקופי (10-6 מטר) ונפרשים עד למרחק שאור חלף מאז ראשית היקום (1023 ק"מ). הצפיפות האסטרונומית נעה בין דלילות החומר הבין גלקטי שצפיפותו רק 10-19 ק"ג/מטר מעוקב, ועד לצפיפות אדירה בתוך חור שחור שעשויה להגיע לכדי 1018 ק"ג למטר מעוקב. ההבדל בין מדידות הצפיפות מגיע לכדי 1037, כלומר 10 ואחריו 37 אפסים! עם הבדלים גדולים שכאלה, אין זה פלא שאסטרונומים החליטו להשתמש בסימון מדעי.
שימו לב למספר הספרות המשמעותיות, או בספרות שאינן אפס, במדידה מדעית. לדוגמה, נסתכל על המספרים 13,000 ק"מ ו 12,756 ק"מ. בסימון מדעי, היינו כותבים את המספרים האלה כך:
4 1.3X10 ק"מ ו 4 1.2756X10 ק"מ
המספר הראשון מרמז למדידה גסה למדי; אי-הודאות במספר זה נעה בין 12,000 ל- 14,000, זהו הבדל של 15 אחוזים. אבל המספר השני מרמז על מדידה מדויקת למדי; אי הודאות היא בין 12,755 לבין 12,757, וזה הבדל של שבר אחוז זעיר. לכן מספר הספרות המשמעותיות מצביע על מידת הדיוק בעת ביצוע המדידה. שימו לב כי מחשבון לעתים קרובות עשוי להחזיר מספר גדול של ספרות משמעותיות, אבל אין זה אומר שניתן להסיק מכך על דיוק גבוה בביצוע מדידה. הדיוק של מספר במדע תלוי באופן בו בוצעה המדידה.
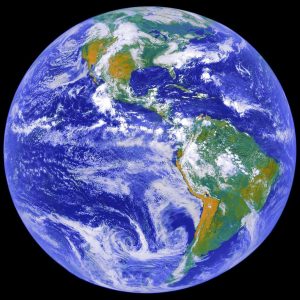
צולם מחללית GOES-8 בתאריך 9.2.1994
באדיבות NASA
עם זאת, יש לציין כי מספרים מדויקים אינם נדרשים תמיד במדע ולעתים אף לא ניתן לבצע מדידה כלל. לעיתים מדידות אטומיות מגיעות לדיוק של 12 ספרות משמעותיות (חלק אחד בטריליון), בעוד שמספרים מסוימים בקוסמולוגיה מדויקים רק עד כדי ספרה משמעותית אחת. ניתן להבין את נושאי הלימוד באסטרונומיה מבלי להתמודד עם מספרים מדויקים מאוד. בדוגמה שניתנה, חשוב יותר לזכור כי קוטר כדור הארץ הוא בערך 13,000 קילומטרים, במקום לשנן את ערכו המדויק 12,756 ק"מ. מספר קטן של גדלים אסטרונומיה ידועים בדיוק גדול יותר משלוש ספרות משמעותיות. לפעמים חוסר הוודאות נמדד בחזקות של עשר, הנקראות "סדר גודל". לעתים די לדעת ערך מקורב של גודל אסטרונומי כך שניתן להעריך אפקטים רבים ללא חישובים מקיפים או חיפוש מדוקדק בספרים. מיומנות מדעית בסיסית זו נקראת אמידה (הערכה). האמידה חוסכת זמן ומאפשרת למדענים להבחין בין השערות מבטיחות לבין השערות אחרות מטופשות למדי.

