השימוש בשנת האור ובפארסק למדידת המרחקים לכוכבים נותן תחושה של מרחקים עצומים. לתרבויות עתיקות, לעומת זאת, הכוכבים נראו קרובים יחסית לכדור הארץ. המצרים דמיינו אותם כנקודות אור על חופה של אוהל גדול, המוחזקת על ידי רכסי הרים בקצות הממלכה. היוונים חשבו עליהם כעל גחלים לוהטות שנישאו על גבי קליפות גבישיות. תרבויות עתיקות לא יכלו להעלות על הדעת כי המרחקים לכוכבים גדולים בהרבה מגודלו של כדור הארץ. אפילו לצופה המודרני, הכוכבים בשמי הלילה נראים כולם במרחק זהה – עומק החלל אינו ברור.
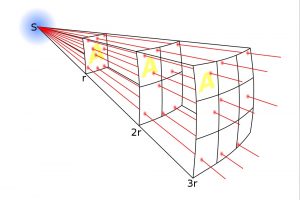
באדיבות Chris Impey
הערכות המרחק לכוכבים בראשית המדע לא היו אלא ניחושים מושכלים. בסוף המאה ה -17, המדען ההולנדי כריסטיאן הויגנס יצר תמונה של השמש באמצעות חריר בחדר חשוך. הוא הגדיל את החור עד שהתמונה נראתה שווה בבהירותה לזו של סיריוס, הכוכב הבהיר ביותר בשמי הלילה. מאחר שהנקב איפשר כניסה רק של 1/27,000 מאור השמש, הויגנס הניח כי סיריוס נמצא במרחק הגדול פי 27,000 ממרחק השמש (למעשה סיריוס נמצא במרחק הגדול פי 543,900 פעמים ממרחק השמש, והוא מאיר יותר מהשמש). בערך באותו זמן, ניסה אייזק ניוטון להשתמש בשבתאי כסוג של מראה המחזירה את אור השמש, במטרה למדוד את עוצמת השמש. הוא ניחש את אחוז אור השמש המוחזר ע"י שבתאי והניח כי לכוכבים בהירים יש בהירות מוחלטת דומה לזו של השמש. ניוטון הגיע למסקנה שהכוכבים הבהירים נמצאים במרחק של כ- 18,000 פעמים רחוק יותר מהשמש (דבר שפשוט אינו נכון, מאותה סיבה שהויגנס אינו צודק: אף אחד מהם לא ידע שרוב הכוכבים הבהירים בשמי הלילה בהירים הרבה יותר מהשמש).
שני החוקרים הללו, ניסו להשתמש בשיטה גסה להערכת המרחק אל הכוכבים; לפי חוק ההופכי של ריבוע המרחק עבור התפשטות האור. לכוכבים הבהירים ביותר יש בהירות נראית הקטנה ב- 10 מיליארד (או 1010) פעמים חלשה יותר מזו של השמש. למרבה הצער, בלתי אפשרי למדוד במדויק את הבהירות היחסית של השמש ושל כוכבים אחרים ללא ציוד מדעי. הטעויות נמשכו גם בתקופה מודרניות. ב- 1829 השתמש המדען האנגלי ויליאם וולסטון בחוק ההופכי של ריבוע המרחק כדי להעריך את מרחקם של רוב הכוכבים הטיפוסיים להערכתו מרחקם גודל פי 100,000 (או 105) ממרחק השמש, שכן חוק ההופכי של ריבוע המרחק מציין כי עמעום של 10 מיליארד פעמים מתאים למרחק הגדול פי 100,000 (וזה מדויק עבור כמה כוכבים).
אומדני מרחק פשוטים המבוססים על הבהירות היחסית של השמש והכוכבים פגומים מסיבה פשוטה אחת: כוכבים פולטים כמויות אור שונות ולכן הנגיהות שלהם שונה. הכוכבים הבהירים בשמים פולטים כמות אור גדולה בהרבה מזו שפולטת השמש, ולכן הם רחוקים הרבה יותר מכפי שחשבו בהנחה שהם דומים לשמש. כמו כן, אומדנים אלה רק נותנים מרחקים טיפוסיים ולא מרחקים מדויקים עבור כוכבים בודדים. אף על פי כן, זוהי דוגמה לאופן שבו רעיון פיזיקלי פשוט מסייע במדידות – הדרך שבה עוצמת האור דועכת כאשר האור מתפשט בחלל – יכול לסייע בהערכת המרחק לכוכבים. גלילאו השתמש בהיגיון זה כאשר הוא כיוון את הטלסקופ שלו אל שביל החלב וראה את האור הרפה של נקודות אור רבות. הוא שיער שהם כולם כוכבים הדומים לשמש, והוא זיהה את עומק החלל העצום התלת-ממדי. באותו זמן, זו הייתה מהפיכה מחשבתית, השתמע ממנה שהיקום גדול אלפי מונים מהאומדנים של המדע היווני!
אחד העיכובים גדולים ביותר במעבר ממודל גיאוצנטרי למודל הליוצנטרי של מערכת השמש היה קשור בחוסר התנועה הנצפית של כוכבים. פארלקסה כוכבית ניתנת למדידה – כאשר כדור הארץ מקיף את השמש. פירושו היה שמרחקי הכוכבים חייבים להיות גדולים מעבר לכל דמיון. המדידה המוצלחת הראשונה של פארלקסה כוכבית בוצעה רק ב- 1838, כאשר האסטרונום הגרמני פרידריך בסל זיהה את שינוי עונתי הקל במיקומו של הכוכב 61 Cygni – רק שני שלישים של שניית קשת. המדידה של מרחק הפארלקסה היא טכניקה טריגונומטית, שאינה תלויה בהנחה כלשהי לגבי טבעו של הכוכב הנצפה. נזכיר כי פארלקסה היא השינוי הזוויתי במצב של גוף שנגרם בעקבות השינוי במיקום של הצופה. חישוב מרחק פארלקסה הוא יישום נוסף של משוואת הזווית הקטנות. המרחק נמצא ביחס הפוך לגודל זווית הפארלקסה. כוכב עם זווית פארלקסה של שניית קשת אחת נמצא במרחק של 1 פארסק.

הכוכב "נע" על רקע הכוכבים הרחוקים, בשל תזוזת הצופה בכדור הארץ.
באדיבות וויקיפדיה
כדי להבין כיצד נעשות מדידות פארלקסה, החזק את האצבע מול הפנים והסתכל מעבר לה לעבר כוננית בצד השני של החדר. האצבע מייצגת כוכב סמוך – הספרים על הקיר הרחוק מייצגים כוכבים רחוקים. העין הימנית שלך מייצגת צופה בצד אחד של השמש. העין השמאלית מייצגת את מיקום הצופה כעבור שישה חודשים, לאחר שכדור הארץ נע לנקודה בצד הנגדי של השמש (שינוי במיקום כדור הארץ שווה לשינוי בשתי יחידות אסטרונומיות). עצום עין אחת ולאחר מכן את השנייה. האצבע שלך (הכוכב הסמוך) תראה כאילו היא נעה ימינה ושמאלה (למרות שהיא לא זזה). שנה את מרחק האצבע מהפנים. בתחילה החזק את אצבעך רק כמה סנטימטרים מעינייך; תתקבל סטייה גדולה. לאחר מכן פשוט את הזרוע וחזור על עצימת עינים לסרוגין; תתקבל סטייה קטנה יותר. ככל שהכוכב קרוב יותר, כך זווית הפארלקסה גדולה יותר. בניסוי זה ניתן למדוד את הפארלקסה במעלות, אבל הפארלקסה של כוכבים קטנה משניית קשת! ניתן למדוד באופן אמין פארלקסה קטנה עד כי 1/100 שניית קשת, ואז המרחק של הכוכב הוא 100 פארסק.
המרחק של כוכב בפארסק הוא ההופכי של זווית פארלקסה שלה בשניות של קשת. זה מסביר את המקור של המונח par-sec: זה המרחק פארלקסה של שניית קשת אחת. אם כוכב רחוק מדי, הפרלקסה שלו קטנה מכדי שניתן יהיה למדוד אותה. (צפה אל האופק כדי לראות מעבר של גוף רחוק – ככל שהגוף מתרחק קשה להבחין בתנועתו, מעבר למרחק מסוים, לא ניתן לשים לב לתנועת הגוף). פרלקסה קטנה יותר מ- 1/100 שניית קשת לא ניתנת למדידה מדויקת, בשל הטשטוש שיוצרת האטמוספירה של כדור הארץ. לכן כוכבים הרחוקים יותר מ- 100 פארסק נמצאים מעבר לגבול מדידה אמינה.
מדעני סוכנות החלל האירופית ניסו להתגבר על המגבלה הזו כאשר שיגרו את לוויין Hipparcos ב- 1989. המשימה שלו הייתה למדוד את הפארלקסה בתנאי הצפייה המדויקים של החלל. כישלון אומלל בהפעלת המנוע הרקטי הציב את הלווין במסלול אליפטי מאוד, שגרם לגלאים להפסיק לפעול כשהם עברו שוב ושוב דרך הקרינה שמסביב לכדור הארץ. למרות זאת, Hipparcos מדד בהצלחה את פארלקסה של 120,000 כוכבים. בנוסף לפארלקסה, הוא מדד במדויק את תנועות הכוכבים האלה, ונתן לנו מידע על האופן שבו הם נעים, אובחנו מערכות כוכבים מרובות ושינויים בהירותם של כוכבים במשך הזמן. לאחרונה, ESA השיקה את המשימה Gaia, במטרה לשפר באופן משמעותי את גודל המדגם ואת הדיוק של מדידות פארלקסה. פרוייקט גאיה שואף לבנות מפה תלת מימדית של כמעט מיליארד כוכבים, ולהגיע לדיוק של 20 מיליוניות של שניית קשת. זוהי הזווית שבה נראית רוחב שערת אדם במרחק של 300 ק"מ!
ידיעת המרחקים המדויקים לכוכבים היא דרישה חשובה ביותר המאפשרת מדידת תכונות אחרות של כוכבים. משמעות הדבר היא כי 20,000 עד 25,000 כוכבים שמרחקם קטן מ- 100 פארסק הם המדגם הסטטיסטי העיקרי שלנו למדידת תכונות הכוכביים. שימו לב שגם מדגם גדול מזה אינו מספיק כדי שנוכל למדוד את המרחק לכמה סוגי כוכבים נדירים. טכניקות אחרות פותחו על מנת לאמוד מרחקים לכוכבים מרוחקים יותר, אך כולן תלויות בסופו של דבר ברמת הדיוק של מדידת הפארלקסה של כוכבים סמוכים.
Author: Chris Impey

