ניוטון סיכם את מדע התנועה בשלושה חוקים. הייתה לו תובנה נוספת, המבוססת על מושג התנע. התנע מוגדר פשוט כמכפלה של מסה במהירות:
תנע = Mv
בדרך כלל אנו מכנים גודל פיזיקלי זה כתנע קווי מפני שהוא מתייחס לתנועה בקו ישר. תנע משלב מסה ותנועה. לגוף נייח אין תנע. ככל שהגוף נע מהר יותר, כך התנע גדול יותר, וככל שהמסה גדולה יותר, כך התנע גדול יותר. הרעיון מוכר לך: למכונית הנעה ב- 20 קמ"ש יש תנע רב יותר מאשר לרוכב אופניים נע במהירות 20 קמ"ש, ובהתאם כמות הנזק שהיא יכולה לגרום! ניוטון ידע כי התנע יכול להשתנות כאשר חפצים מתנגשים או יוצרים אינטראקציה ביניהם. אבל הוא הבין כי הסכום הכולל של התנע יישאר זהה לפני ואחרי ההתנגשות. זהו חוק שימור התנע.

באדיבות pixabay
אם אתה מחזיק אקדח אין לו תנע. לאחר ירייה, הכדור נע במהירות גבוהה מאוד ולכן התנע שלו הוא מכפלה של מסה קטנה מאוד ומהירות גדולה מאוד. הרתיעה של האקדח היא בדיוק באותו תנע אך בכיוון ההפוך – כך שסכום התנעים של הקליע והאקדח שווה לאפס כפי שהיה טרם הירי. כדי לשמור על רתיעה קטנה, האקדח כבד, כך שהתנע שלו הוא מכפלה של מסה גדולה ומהירות קטנה. נקודת המפתח היא שהסכום הכולל של התנע לא השתנה. תנע אפס לפני כן הפך לסכום של שני תנעים שגם הוא אפס. אפקט דומה בזמן החלקה על קרח כאשר הגולש זורק חפץ כבד. התנע שהוענק לסלע יתאזן בתנע שווה שבו ינוע הגולש בכיוון ההפוך. אבל מכיוון שהמסה של הגולש גדולה יותר, מהירותו לאחור תהיה קטנה יותר ממהירות החפץ הנע קדימה.
אנשים רבים תוהים כיצד נעים טילים. איך הם מצליחים להישאר באוויר? כיצד הטיל "נדחף" כאשר הוא בחלל? התשובה ברורה אם חושבים על התנע. כדי ליצור תנועה ותנע כלפי מעלה לרקטה, הדלק שנשרף נפלט במהירות גבוהה לאחור. למעשה, נחירי הרקטות וסילון הגז הנפלט מהן נועדו לנצל ככל האפשר את מהירות היציאה הגבוהה של הגז. בכל נקודה בטיסה של הטיל, התנע הקדמי של הטיל מאוזן בדיוק על ידי התנע בכיוון ההפוך של אדי הדלק. לרקטה יש מסה גדולה, והגז בעל מסה קטנה ומהירות גבוהה. לכן, אין זה משנה אם הרקטה נמצאת באוויר או בחלל ריק!
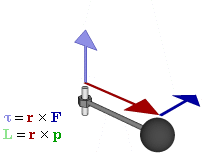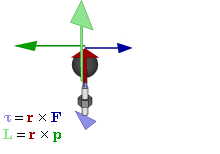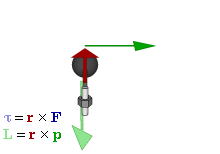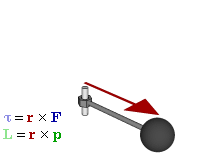
באדיבות וויקיפדיה
התנע הזוויתי דומה לתנע ליניארי, אבל הוא אופייני לסיבוב או לתנועה במסלולים בהם פועל כוח מרכזי ככוח הכבידה. הוא מוגדר כתוצר של מסה, מהירות והרדיוס או המרחק ממקור הכוח המרכזי:
תנע זוויתי = M v r
במקרה זה הרדיוס הוא בגודל של הגוף מסתובב או המרחק של גוף המקיף את מרכז הכובד. חוק השימור של התנע הזוויתי אומר כי התנע הזוויתי של מערכת יישאר קבוע גם במהלך השינויים של תצורת המערכת.
אם מערכת השמש באמת נוצרה מענן גז קורס שהשתרע לפחות עד למסלולים של נפטון ופלוטו, אזי מהירות הסיבוב בוודאי עלתה במידה ניכרת עם ההתכווצות. בכמה? המרחק הממוצע של נפטון מהשמש הוא 30 יחידות אסטרונומיות, או 30 × 1.5 × 108 = 4.5 × 109 ק"מ. אם נניח כי כל החומר בתוך רדיוס מסלול זה הסתיים בשמש, אז אחרי קריסת הגודל של הענן הוא רק רדיוס השמש, או 700,000 ק"מ. במהלך קריסה זו, המסה לא השתנתה. אז אם הרדיוס r קטן פי
6500 = 700,000 / 109 4.5x
אזי מהירות הסיבוב חייבת לגדול באותו יחס. מסתבר שהשמש אינה מסתובבת בקצב כה גבוה כפי שהיינו מצפים, ומשאירה אותנו עם תעלומה בהבנתנו את היווצרותה של מערכת השמש.
דוגמה נוספת לשינוי התנע הזוויתי היא כדור הארץ במסלולו של השמש. מסלול כדור הארץ סוטה ממסלול מעגלי ב- 3.4%. משמעות הדבר היא שהיא משתנה בין 1.017 פעמים המרחק הממוצע של כדור הארץ-השמש ל- 0.983 פעמים ממוצע המרחק בין כדור הארץ לשמש. היות והתנע הזוויתי נשמר, כאשר המרחק גדל מהירות צריכה לרדת, וכאשר המרחק קטן מהירות צריכה לגדול. המהירות הממוצעת של כדור הארץ היא 2πr / (Time in a year) = (2 × 3.14 × 1.5 × 108) / (365 × 24 × 3600) = 14.94 ק"מ לשנייה. לכן, כאשר כדור הארץ קרוב ביותר לשמש, מהירותו היא 14.94 × 1.017 = 15.18 ק"מ לשנייה. כאשר היא רחוקה מהשמש מהירותה 14.93 × 0.983 = 14.69 ק"מ לשנייה. זהו שינוי קל במהירות המסלולית המשפיע על הזמן המבוסס על מיקום הכוכבים.
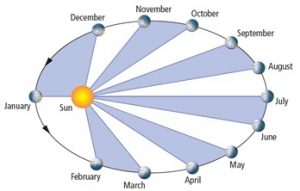
באדיבות וויקיפדיה
יש הסבר קונקרטי ופיזי לחוק השני של קפלר של תנועה פלנטרית. חוק זה אומר כי קו דמיוני שמחבר את כוכב לכת (או שביט או כל גוף אחר המקיף את השמש) אל השמש חולף על פני אזורים שווים במרווחים שווים של זמן. חוק קפלר אינו אלא פן נוסף של חוק שימור התנע הזוויתי. המהירות המסלולית תלוי במרחק אל השמש, אבל שניהם משתנים תוך שמירה על תנע זוויתי קבוע.
Author: Chris Impey

