יוהנס קפלר פרסם את תגליותיו על מסלולי כוכבי הלכת בשני ספרים, ב -1609 וב -1619. ממצאיו יכולים להיות מזוקקים לשלושה "חוקים" מפורסמים וכלליים, שנקראו "חוקי התנועה הפלנטרית" של קפלר. חוקי קפלר חזקים משום שהם כלליים. הם פשוט הרחבה של חוקי התנועה של ניוטון, כאשר שני גופים קשורים זה בזה באופן גרוויטציוני (אם כי הם קדמו לניוטון!). חוקי קפלר חלים על כל תנועה מסלולית, בין אם היא סביב כוכב לכת או סביב השמש, הירח סביב כדור הארץ, הארץ סביב השמש, או כוכב סביב מרכז הגלקסיה.
החוק הראשון של קפלר הוא פשוט: כל מסלולי כוכבי הלכת הם אליפסות, כאשר השמש נמצאת באחת מנקודות המוקד. חרף פשטות החוק הוא תפסו אנשים רבים שנרדמו על משמרתם. הפילוסוף אריסטו הכריז על המעגל כצורת מסלול מושלמת, ואפלטון העלה צורות אידיאליות רבות אחרות. האליפסה לא היתה ברשימות שלהם! לאחר שאובחנה צורה זו, היה אפשר פתאום להבין את מיקומי פלנטות במדויק.
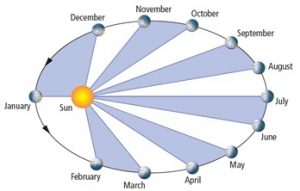
באדיבות וויקיפדיה
החוקים השני והשלישי היו תוצאה של ניסיונות של קפלר למצוא תבניות המאפינות את המסלולים של כוכבי הלכת. החוקים השני והשלישי של קפלר הם יחסים מתמטיים בין המרחק של כוכב לכת מהשמש לבין קצב תנועתו סביב השמש. שתי התוצאות הן תוצאה טבעית של החלת חוק הכובד של ניוטון וחוק שימור התנע הזוויתי, לאובייקט הנע על במסלול אליפטי, אך קפלר הצליח להפתיע כאשר ניסח אותם ללא מושגים אלה!
החוק השני של קפלר העוסק תנועה פלנטרית קובע כי כוכב לכת מאיץ כאשר הוא קרוב לשמש ומאט כאשר הוא רחוק ממנה. במילים אחרות, אם אתה מדמיין קו המחבר בין כוכב לכת לשמש, הקו חולף על פני אזורים שווים במרווחי זמן שווים. זוהי תוצאה פשוטה של שימור התנע הזוויתי. התנע הזוויתי של כוכב הלכת ביחס לשמש, נשומר כל הזמן. לכן, כאשר הכוכב קרוב יותר לשמש, הוא חייב לנוע מהר יותר כדי לשמור על התנע הזוויתי. (תזכורת , התנע הזוויתי הוא L = r × m v)
החוק השלישי של קפלר קובע כי הריבוע של זמן המחזור של פלנטה (P) נמצא ביחס ישר לחזקה השלישית של מחצית הציר המרכזי:
P2 α a3
במשוואה זו, P היא זמן המחזור, ו- a הוא מחצית הציר המרכזי. עבור מערכת השמש שלנו, ניתן לקבוע את קבועי הפרופורציה של המשוואה לאחר שנשתמש ביחידות של שנים עבור זמן מחזור, וויחידות אסטרונומיות עבור הציר המרכזי (1AU = ממוצע המרחק בין כדור הארץ לשמש = הציר המרכזי של כדור הארץ). במקרה הזה:
(P Years)2 = (aAU)3
המרחק הממוצע של מאדים מהשמש הוא בערך 50% יותר מאשר מרחק כדור הארץ מהשמש, או 1.52AU לכן זמן המחזור שלו בריבוע שווה ל 3(1.52) = 3.51, וזמן המחזור הוא (3.52)√ = 1.87 שנים. שנת מאדים כמעט פי שניים משנת כדור הארץ. החוק השלישי של קפלר מתאר גידול שיטתית בזמן המחזור של הפלנטות עם גידול המרחק שלהן מהשמש. שימו לב כי בחישובים אלה אנו משתמשים רק בשלוש ספרות משמעותיות. הסיבה לכך היא כי יש חריגות מן החוקים של קפלר ברמת דיוק העולה על 0.1%.
בואו נציג עוד כמה יישומים של קשר חשוב זה. נניח שאנחנו יכולים להשתמש בגיאומטריה כדי להראות כי צדק רחוק מהשמש פי 5.2 פעמים מאשר כדור הארץ. מהו זמן המחזור של צדק? בעקבות הדוגמה הקודמת, המרחק בשלישית שווה ל 3(5.2) = 140.6, וזמן המחזור הוא שורש התוצאה האחרונה (140.6) √ = 11.9 שנים. שנת הצדק היא כמעט פי 12 פעמים משנת כדור הארץ. עכשיו בואו נדמיין כי עם תצפית זהירה הצלחנו למצוא כי זמן המחזור של מרקורי במסלולו סביב השמש הוא 89 ימים. נמיר לשנים, נחשב את מרחקו הממוצע של מרקיורי מהשמש בשני שלבים 2(89/365) = 0.0595, ולכן המרחק הממוצע של מרקיורי מהשמש הוא 1/3(0.0595) = 0.39AU. מרקורי נמצא במרחק השווה לקצת יותר משליש מרחקו כדור הארץ מהשמש.
עבודתו של קפלר קידמה מאוד את הרעיונות של קופרניקוס, לפיהםכל כוכבי הלכת נעים במסלולים סביב השמש, במקום סביב כדור הארץ. היחסים הפשוטים שלו לתיאור מסלולי הפלנטות הבהירו כי השמש שולטת בתנועות הפלנטריות, ולא כדור הארץ. רעיון האליפסות של קפלר סילק את כל הסיבוכים של הקוסמולוגיה הגיאוצנטרית, ובמיוחד את מערכת גלגלי העזר של תלמי ואת חישוביו המורכבים. חשוב יותר, מערכת פשוטה זו היתה מסוגלת לחזות בדיוק גבוה יותר את המיקום של כוכבי הלכת. התיאור עדיין לא היה מושלם, אבל היה זה צעד גדול קדימה בכיוון הנכון. נדרשו חוקי ניוטון כדי לאפשר תיקונים במסלולי הפלנטות בשל השפעת הכבידה של כוכבי הלכת זה על זה, ותורת היחסות של אינשטיין היתה נחוצה כדי להסביר את פרטי תנועתו המהירה של מרקורי סמוך לשמש. העבודה השיטתית של שלושת האנשים האלה מראה שהמדע הוא תהליך, תוך ביצוע עבודה רציפה ושיפור תגליות העבר.