קפלר הסביר את סדירות תנועת הפלנטות באמצעות מסלולים אליפטיים. הוא גילה מערכת יחסים בין זמן המחזור (או זמן הקפה) של שביט לבין מחצית הציר המרכזי (או חצי מהציר הארוך של המסלול) a. אם זמן המחזור P נמדד בשנים ומחצית הציר המרכזי a נמדדת ביחידות אסטרונומיות, נקבל:
(PYears)2 = (aA.U.)3
ברור שזה נכון עבור כדור הארץ, שכן המשוואה תיתן 13 = 12, וזה נכון. (כתרגיל אתה יכול לאמת את זה עבור כוכבי לכת אחרים גם כן.) קפלר הגיע אל תגליותיו בנושא צורת המסלולים הפלנטריים הרבה לפני שהאלי זיהה כי שביטים הם תופעות מחזוריות. אבל הקשר לעיל נכון עבור כל תנועה סביב השמש, כולל מסלולים של שביטים. לדוגמה, כירון (סווג בתחילה כאסטרואיד אבל כיום מוכר כשביט) נע על מסלול אליפטי בין שבתאי אורנוס, עם מחצית ציר מרכזי שגודלה 13.7 יחידות אסטרונומיות. החזקה השלישית של מספר זה היא 2571. לכן, אם זמן המחזור בריבוע הוא 2571, שזמן המחזור שלוו הוא: 1/2(2571) = 51 שנים. זהו בדיוק הזמן שבו כירון מקיף את השמש.
ניתן להשתמש בחוק השלישי של קפלר למצוא מרחקים באמצעות זמני מחזור. לדוגמה, אנו יודעים כי השביט של האלי חוזר בכל 75 שנים. מהו מרחקו הממוצע מהשמש? הריבוע של זמן המחזור הוא 5625. לכן, החזקה השלישית של מחצית הציר המרכזי ביחידות אסטרונומיות היא 5625. אם נוציא את השורש השלישי של מספר זה באמצעות מחשבון, נקבל שמחצית הציר המרכזי היא בערך 18 יחידות אסטרונומיות, או כמעט מרחקו של אורנוס מהשמש.
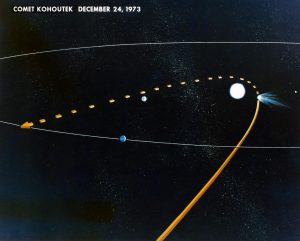
באדיבות NASA
מה הכוונה למרחק הממוצע של מסלול? לפלנטות אין מסלולים אליפטיים קיצוניים; המסלולים נראים כמו מעגלים מעוכים. במקרה זה, מוקדי האליפסה קרובים זה לזה, האקסצנטריות קרובה לאפס, והציר המרכזי למחצה אינו שונה בהרבה מרדיוס של מסלול מעגלי. מסלולי השביט שונים לחלוטין. האליפסות שלהם מוארכות מאוד והאקסצנטריות שלהם קרובה לאחד. מוקדי האליפסה מרוחקים זה מזה. למעשה, המרחק בנקודה הקרובה ביותר לשמש עשוי להיות קטן בהרבה ממחצית הציר הראשי. לכן, בקירוב טוב ניתן לומר שהמרחק המרבי מהשמש הוא פעמיים מחצית הציר המרכזי. המיקום המרוחק ביותר של שביט האלי מהשמש הוא בערך 36 יחידות אסטרונומיות, בין מסלולי נפטון ופלוטו.
שביטים בחגורת קויפר וענן אורט נמצאים במרחקים של 100 ו- ,000100. מה יהיה זמן המחזור של שביטים אלה? זכור כי המרחק המרבי הוא פעמיים ציר חצי מרכזי. אם אתה מכניס את ערכי מחצית הציר מרכזי של 50 ו- 50,000 במשוואה עבור החוק השלישי של קפלר, ניתן לקבל את זמני המחזור של כ- 350 שנים ו- 11 מיליון שנים, בהתאמה!
בתקופה הארוכה ובהארכת המסלולים בענן אורט יש משמעות חשובה. החוק השני של קפלר קובע כי רדיוס וקטור של גוף המקיף את השמש יכסה שטחים שווים באותו פרק זמן. עם מסלול אליפטי מאוד, זה אומר שביט חייב לנוע הרבה יותר לאט כאשר הוא רחוק מהשמש מאשר כאשר הוא קרוב לשמש. כמה איטי יותר? חוק הכבידה העולמי של ניוטון יכול לסייע בפיתוח הקשר של המהירות במסלול מעגלי:
![]()
במשוואה זו, G הוא קבוע הכבידה ו- M הוא מסת השמש. אנחנו יכולים לשער את התשובה רק על ידי קנה המידה של יחס זה שבו v a 1/r. אם נבחן את היחסים כך ש- G ו- M יתבטלו, נקבל:
vEarth / vcomet = (rcomet / rEarth)1/2
במרחק של יחידה אסטרונומית אחת מהשמש לכדור הארץ יש מהירות מסלולית של כ -30 ק"מ לשנייה. אז במרחק 50,000 יחידות אסטרונומיות, לשביט תהיה מהירות מסלולית של
(30 / 50,000)1/2 = 0.73 km/s
התוצאה היא כי שביט מבלה את מרבית זמנו כאשר הוא זוחל במסלולו במרחק עצום מן השמש. שביט שזמן המחזור שלו כמיליון שנים יבלה רק שנה או שנתיים בתוך מערכת השמש הפנימית.

