הצעד המבריק ביותר של ניוטון היה לקשר בין התנועות על פני כדור הארץ לתנועות גרמי השמים. הוא ידע שכוח חייב לגרום לגוף, למשל תפוח, ליפול לכדור הארץ. הוא גם ידע כי גם על הירח חייב לפעול כוח כדי לגרום לו לנוע במסלול מעגלי כאשר הוא מקיף את כדור הארץ. האם יכול להיות שאותו כוח פועל גם על התפוח וגם על הירח? (לא ידוע האם הסיפור על ניוטון הזוכה לתובנה במהלך התבוננות בתפוח נופל נכון. אבל, קיים מטע תפוחים בסמוך לבית בו נולד ניוטון באנגליה!) חוק כוח הכבידה העולמי הוא אחד הגילויים החשובים ביותר בהיסטוריה של המדע.
ניוטון ביטא את חוקיו במתמטיקה. במילים, אנו יכולים לכתוב: כל חלקיק ביקום מושך כל חלקיק אחר בכוח הנמצא ביחס ישר למכפלת המסות של החלקיקים, וביחס הפוך לריבוע המרחק בין החלקיקים. אנו מגדירים את כוח הכבידה ככוח משיכה עולמי; כלומר זוהי תכונה הקיימת בכל עצם ביקום. ביטוי זה של כוח הכבידה אומר שאם ניתן היה להכפיל את מסת השמש, כוח המשיכה שבו השמש הייתה מושכת את כדור הארץ היה מוכפל. כמו כן הכפלת המרחק ביניהם, הייתה גורמת להקטנת הכוח פי ארבעה (שניים בחזקת שניים). באופן דומה, אם מסת השמש תגדל פי שלוש, הכוח יגדל פי שלוש, אבל אם המרחק יגדל פי שלוש, הכוח יקטן פי תשע.
כוח הכבידה הוא כוח המציית לחוק ההופכי של ריבוע המרחק. כלומר, הכוח פוחת יחסית לריבוע המרחק מן הגוף. ניוטון היה מסוגל להראות כי אם כוח הכבידה קטן בהתאם לחוק ריבוע המרחק, אזי מסלולי הפלנטות חייבים להיות אליפסות כאשר השמש באחד המוקדים. כאן הופיע סוף סוף הסבר אלגנטי לעבודה של קפלר. באמצעות חוק הכבידה העולמי של ניוטון ניתן היה לחזות בהצלחה את מועד חזרתו של כוכב שביט האלי במסלולו האליפטי סביב השמש – אישור מדהים לתיאוריה.
חוק הכבידה של ניוטון חל על כל שני גופים נפרדים. כיצד נוכל לחשב את כוח הכבידה על האדם, כאשר פועל עליו כוח משיכה של כל החלקים השונים המרכיבים את כדור הארץ? ניוטון המציא את החשבון הדיפרנציאלי והאינטגרלי (חדו"א או החשבון האינפיניטסימלי) כדי לפתור בעיה זו. באמצעות החדו"א התקבלה תוצאה כי גוף כדורי כמו פלנטה מתנהג כאילו כל המסה שלו נמצאת במרכזו. ניוטון ערף חישובים רבים בעלי ערך, אך אז קבר אותם במגירת שולחנו, בעוד מוחו הרעבתני מוצא בעיות חדשות להתמודד עמן. בעידודו של אדמונד האלי, האסטרונום המפורסם, הוא נאות לפרסם לבסוף את עבודתו בספר מאסטר בשם "Principia" (עקרונות), בשנת 1687.
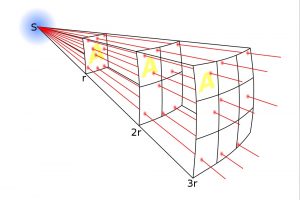
חוק הכבידה האוניברסלי של ניוטון שייך לסוג נפוץ של חוקים הנקראים חוק ריבועי הפוך. תלות זו אופיינית לכוחות רבים הנובעים מנקודה, למעשה, זוהי תכונה של המרחב התלת-ממדי שאנו חיים בו. אנו יכולים לדמיין קווי כוח כבידה היוצאים בגוף כלשהו לכל הכיוונים. מידת הריכוז של קווי הכוח מייצגת את עוצמת כוח הכובד. צפיפות גבוהה מעידה על כוח חזק.
שטח הפנים של כל מעטפת כדורית סביב הגוף היא:
4πD2
כאשר D הוא המרחק מהגוף.
קווי הכוח מתפשטים יותר ויותר כשאנחנו מתרחקים מן הגוף. צפיפות הקווים יורדת בהתאמה לירידת העוצמה של כוח הכבידה. המספר הכולל של קווי הכוח הנובעים מהגוף קבוע, אבל הם מתפשטים על שטח ההולך וגדל הנמצא ביחס יחס ל D2 לכן צפיפות קווי הכוח באזור מסוים הולכת ופוחתת עם הריבוע ההופכי של המרחק, כלומר פרופורציונלי לאחד חלקי D2 .
כוחות חשמליים ומגנטיים מצייתים לאותה חוקיות של עוצמה הדועכת עם המרחק כמו כוח הכבידה. ניתן להבין איך החוק ההופכי של ריבוע המרחק חל גם על קרינה ממנורה. תארו לעצמכם קרני אור היוצאות ממקור אור. אם במרחק מסוים, האור הנפלט בכיוון מסוים מתפשט על יחידה אחת, ולאחר מכן, במרווח כפול, הוא משתרע על ארבע יחידות. עוצמת האור במרחק יורדת ל- 1/4 מעוצמתה הקודמת. באותו אופן, עוצמת האור במרחק הגדול פי שלוש מהמרחק הראשוני היא 1/9 מהעוצמה הראשונה. בדומה לכוח הכבידה, גם הקרינה הנובעת ממנורה מצייתת לחוק הריבוע ההפוך.
נציג את דרך החשיבה של אייזיק ניוטון. ניוטון השתמש בחוק ההופכי כדי לחשב את תנועת תפוח נופל. באותו אופן הוא השתמש באותו חוק לחישוב תנועת הירח סביב כדור הארץ. נשתמש בגיאומטריה פשוטה כדי לקבל תשובה מקורבת לזו של ניוטון, נחוץ חישוב מפורט יותר לתוצאה מדויקת יותר. המרחק ממרכז הירח למרכז כדור הארץ הוא לערך 60 פעמים רדיוס כדור הארץ. לכן, לפי חוק הריבוע ההופכי, כוח הכבידה שכדור הארץ מפעיל על יחידת מסה הנמצאת במרחק של הירח מכדור הארץ, צריך להיות קטן פי 60 בריבוע, מאשר על פני כדור הארץ. מכאן שהתאוצה של הירח הגורמת לו לסטות מן הנתיב הישר ולנוע סביב כדור הארץ היא:
9.8 / 602 = 0.0027 m/s2
מכאן, שבכל שניה הירח נופל במסלולו סביב הארץ מרחק של 0.0014 מטר או רק 1.4 מ"מ לכיוון מרכז כדור הארץ. מהו המרחק שעובר הירח בשנייה אחת במסלולו סביב הארץ? יש לחלק את היקף המסלול בזמן ההקפה. זמן ההקפה של הירח סביב כדור הארץ הוא 27.3 ימים או:
27.3 x 24 x 3600 = 2.36 x 106 seconds
שימו לב שחודש, זמן ההקפה של הירח מנקודת הראות של צופה בכדור הארץ, הוא 29.5 ימים ארוך יותר מזמן ההקפה השמיימי. זאת, מפני שכדור הארץ גם נע במסלולו סביב השמש.
לכן בשנייה אחת הירח עובר:
(2 π 384,000) / 2.36 × 106 = 1.02 km
לצורך חישוב הזווית עבור קטע קטן כל כך של המסלול אנו יכולים להתייחס אל הנתיב המעוקל כמשולש ישר זווית ולהשתמש בטנגנס הזווית כדי לחשב אותה:
tan(a) = 0.0014/1000
מכאן :
a = 0.28877 שניות קשת
ניתן להגיע לתוצאה דומה באמצעות הקרוב לזוויות קטנות והמרה מרדיאניים לשניות קשת:
a/ 206,265 = d / D → a = 206,265 (0.0014 / 1020) = 0.2831 arcsec
זוהי הזווית שבה הירח חורג מסלולו הישר בכל שנייה בשל כוח הכבידה של כדור הארץ.
לחישוב הזווית המרכזית שבה הירח מסתובב במסלולו נשתמש בקירוב עבור זוויות קטנות:
a/ 206,265 = d / D → a = 206,265 (1.02 / 384,000) = 0.5 arcsec
מספר דומה. כך אנו יכולים להראות בחישוב מקורב זה כי חוק הריבוע ההופכי של כוח הכבידה מתאר את מסלול הירח.
למעשה, קל יותר לכתוב את חוק הכבידה במונחים מתמטיים מאשר לפרט אותו במילים. אם יש לנו שתי מסות MA ו MB, שהמרחק ביניהן R אזי חוק הכבידה של ניוטון מתאר את הכוח בין מסה A לבין מסה B באמצעות הביטוי:
F = G MA MB / R2
המספר G הוא קבוע הכבידה, קבוע יסוד של הטבע. אם נמדוד מסה בקילוגרמים, מרחק במטר, וכוח ביחידות ניוטון אזי
G = 6.67 × 10-11 N×m2/kg2
קבוע זה הוא מספר זעיר – כוח הכבידה הוא למעשה כוח חלש מאוד. רק בשל כמויות עצומות של חומר כוח הכבידה הופך לכוח משמעותי.

באדיבות וויקיפדיה
המסה של כדור הארץ, 1024× 6 ק"ג, גורמת לתאוצה כלפי מטה שגודלה 9.8m/s2. אך כל גוף בעל מסה מושך כל גוף אחר בעל מסה, אז מה עם גופים אחרים? נניח ששתי ספינות בעלות מסה של 10,000 טון (107 ק"ג) נמצאות במים והמרחק ביניהן 100 מטר. כוח הכבידה ביניהן הוא:
(6.67 × 10-11 x 107 x 107) / (100) 2 = 0.67 N
נקבל באמצעות חוק התנועה השני של ניוטון, מסה / כוח = תאוצה, כי התאוצה על כל ספינה תהיה 10-8 × 6.7 מטר/שניה2. גודל זעיר מכדי שניתן יהיה למדוד אותו. כוח הכבידה של גופים אסטרונומיים גדול לאין-שיעור מכוח כבידה של גופים יומיומיים! אם אנחנו רוצים להשוות את כוח הכבידה של שני גופים שונים, אנחנו יכולים לבדוק את היחסים ללא צורך בקבוע הכבידה. כדי להשוות את כוח הכבידה היחסי של אובייקטים B ו- C על אובייקט A, נקבל:
FBA / FCA = (MB / MC) x (RCA /RBA)2
ניתן לצמצם את קבוע הכבידה ואת המסה של גוף A. אנחנו לכודים בכדור הארץ באמצעות כוח הכבידה שלו. בואו נשווה את כוח הכבידה של אובייקטים אחרים. באמצעות המשוואה שבה B הוא השמש ו- C הוא כדור הארץ, נבחן את הכוח היחסי על גוף שלישי הנמצא על פני כדור הארץ:
(2 × 1030/6 × 1024) x (6400 / 1.5 × 108) 2 = 6 × 10-4
מכאן שגודל הכוח שמפעילה השמש הוא פחות מעשירית אחוז מכוח הכבידה שמפעיל כדור הארץ עליך. ומה יחס בין הכוח בין שני אנשים היושבים בחדר לכוח שמפעיל עליהם כדור הארץ? אם הם שוקלים 50 ק"ג והם במרחק של מטר אחד זה מזה, הכוח היחסי הוא:
(50/6 × 1024) × (6400 / 0.001) 2 = 2 × 10-9
כוח המשיכה שמפעילים האנשים זה על זה הוא מיליארדית מהכוח מרתק אותם לכדור הארץ. חוק הכבידה העולמי של ניוטון משתלב היטב עם חוקי התנועה שלו. כוח הכבידה הוא הכוח שמחזיק את הירח בתנועתו סביב כדור הארץ, או את כדור הארץ בתנועה סביב השמש. בהעדר כוח הכבידה, כדור הארץ היה פשוט נע בקו ישר בחלל, בדיוק כמו שתנוע אבן המסתחררת על חוט לאחר שהחוט נקרע. בחלל אין חיכוך או התנגדות אוויר, ולכן מערכת השמש יכולה לשמור על תנועותיה לאורך זמן רב מאוד. כמו כן, כוח הכבידה הוא כוח הפועל הדדית בין שני גופים, וממחיש את החוק השלישי של ניוטון. כדור הארץ מפעיל כוח כבידה עלינו, אבל גם אנחנו מפעילים כוח כבידה שווה על כדור הארץ! כוח הכבידה פועל בטווח ארוכים. הוא יורד בריבוע ככל שהמרחק גדל אך אינו מתאפס. באמצעות ההיגיון הזה ניוטון היה בטוח שכוח הכבידה הוא כוח אוניברסלי.
חשוב לזכור את ההבדל בין המסה והמשקל. מסה היא תכונה בסיסית של עצם או חלקיק. זה כמות של "דברים" או מספר האטומים של משהו, הנמדד ביחידות של ק"ג. גורם זה קובע את גודלו של כוח הכובד. משקל תלוי במיקום שלך בחלל. על פני כדור הארץ, התאוצה בשל כוח הכבידה הארצי היא 9.8 מטר/שניה2 בדרך כלל מסומנת בסמל g (להבדיל מהקבוע העולמי G). זוהי עלייה במהירות של 9.8 מטרים לשנייה עבור כל שנייה במהלך נפילה סמוך לפני כדור הארץ. ערכו של g על הירח קטן יותר מפני שהוא מסיבי פחות, התאוצה על פני הירח בשל כוח הכבידה היא רק 1.6 מטר/שניה2 . אם תשקלו 600 ניוטון על כדור הארץ, תשקלו 100 ניוטון על הירח אך מסתכם לא תשתנה. במסלול סביב כדור הארץ, אתה תהיו חסרי משקל. הסיבה לכך היא שגם אתם וגם החללית נופלים באותה תאוצת כבידה, לכן הכוח הפועל בינכם לבין החללית הוא אפס. אתם גם תהיו חסרי משקל הרחק בחלל, כאשר מרחקכם מכל כוכב או או פלנטה יהיה גדול דיו. בכל המצבים האלה המסה שלכם זהה. אבל המשקל שלכם תלוי בכוח הכובד המקומי.
ניוטון האיש הכיל אוסף של סתירות. הוא היה צנוע כאשר הוא חשב על קודמיו. הוא אמר "אם ראיתי יותר מאחרים, הרי זה משום שעמדתי על כתפיהם של ענקים". עם זאת, הוא יכול היה להיות אכזרי עם עמיתים ויריבים. האיש שיצר את ההשקפה הרציונלית והמכניסטית של היקום "כעבודת השעון" הקדיש מאמצים רבים בחקר אלכימיה. לאחר מותו נמצאו באחוזה שלו אלפי עמודים של ניתוח מפורט של התנ"ך. קל יותר לשפוט את ניוטון המדען. הוא השתמש בחוק פשוט אחד כדי להבין מגוון עצום של השפעות בלתי קשורות לכאורה: משקל, תפוח נופל מעץ, הירח הנע סביב כדור הארץ, מסלול השביט או כוכבי הלכת הנעים סביב השמש.
הסופר האנגלי, אלכסנדר פופ כתב את הפסוק החכם הזה בעקבות מותו של ניוטון:
"חוקי הטבע נחו במסתור;
אלוהים אמר "יהי ניוטון" ויהי אור!

