ראיות רבות מצביעות על קיומו של חור שחור סופר-מאסיבי במרכז גלקסיית שביל החלב. למעשה, הראיות לחור השחור בגלקסיה שלנו טובות יותר מהראיות לכל חור שחור אחר, משום שהוא מבוסס על עשרות מסלולי כוכביים, ומהווה דגם מצוין של התפלגות המסה המרכזית. בהתבסס על עקרון הממוצעות, האסטרונומים הניחו שניתן למצוא חורים שחורים סופר-מסיביים בגלקסיות אחרות. הם עמלו קשה כדי לאתר אותם גופים קומפקטיים, ובשנים האחרונות זכו להצלחה רבה. מחקר זהיר של גרעינים בגלקסיות קרובות מגלה ריכוזים קיצוניים של החומר בליבת הגלקסיה. יתר על כן, ניתן להסביר את מהירות מסלולית של גופים בליבת הגלקסיה באמצעות גוף מרכזי צפוף ביותר. יש עדויות גוברות לכך שחורים שחורים סופר-מאסיביים ממוקמים במרכז גלקסיות סמוכות נפוצים יחסית, ולמעשה, מאמינים כי בכל הגלקסיות הקטנות קיימים חורים שחורים סופר-מאסיביים.

באדיבות teachastronomy
העדות הטובה ביותר לחורים שחורים גדולים מסתייעת בספקטרוסקופיה כדי למדוד את המהירות הממוצעת של כוכבים סמוך למרכזי הגלקסיות. אם התנועות מהירות מדי, מכדי שניתן להסבירן באמצעות אוכלוסיות הכוכבים באזורי הגרעין, ניתן להניח כי הגורם לתנועות אלה הוא גוף קומפקטי בדומה לחור שחור. במספר גלקסיות גדל והולך נמצאה עלייה חדה במהירויות הכוכבים בסמוך לגרעיניהן. ניתן להשתמש במהירויות כוכבים כדי "לשקול" גלקסיה בתוך רדיוס מסוים. שיטה זו יעילה ביותר במרכזי הגלקסיות שבהן ניתן לאתר אזור מרכזי קטן באמצעות ספקטרוגרף. שימוש נרחב בטלסקופ החלל האבל נעשה לצורך מחקר זה.
בגלקסיית שביל החלב שלנו, ניתן לעקוב אחר תנועות הכוכבים בחלק הפנימי ביותר של הגלקסיה ולמדוד את מסלולם. עבודה זו נעשתה לראשונה על ידי אנדריאה גז ריינהרט גנזל. טכניקה זו מאפשרת לנו לקבוע באופן ישיר את המסה של החור השחור העל-מאסיבי הנמצא בלב הגלקסיה שלנו. ההערכה היא שמסתו קצת יותר מ- 4 מיליון מסות שמש.

באדיבות teachastronomy
אסטרונומים יכולים לזהות גלקסיות, שבהן נמדדו תנועות מהירות סביב גרעיניהן. השילוב מספק ראיות טובות לחורים שחורים על-מסיביים. פיזור מהירויות מראה כיצד המסה ליד מרכז הגלקסיה משתנה ביחס למרחק. מאידך תצלום מראה כיצד האור הנפלט מהגלקסיות משתנה ביחס למרחק ממרכז הגלקסיה. היחס בין שתי הכמויות מאפשר לזהות את השתנות המסה וכמות האור ביחס למרחק ממרכז הגלקסיה. גלקסיות מסוימות מראות עלייה חדה ביחסי המסה לאור הנפלט ממרכזן בפארסק המרכזי. באוכלוסיות כוכבים סטנדרטיות היחס בין השתנות המסות להשתנות אור נמצא בין 2 ל- 30, ולכן ערכים גבוהים יותר מטווח זה, מצביעים על ריכוז של מסה אפלה. מסה זו קומפקטית ביותר, ולכן היא שונה לגמרי מהחומר האפל המופץ בכמויות גדולות במרחבי הילה של הגלקסיות (אם כי יש חומר אפל במרכזי הגלקסיות, המפוזר בקנה מידה גדול יותר). אסטרונומים ראו עדויות לחורים שחורים מסיביים של כמה מיליוני מסות שמש בגלקסיה שלנו וב- M 32, ואחרים שמסתם מגיעה לכדי מיליארדי מסות שמש ב- M 87, גלקסיה אליפטית ענקית בצביר הבתולה.
למרות שאיננו יכולים למדוד ישירות את תנועות הכוכבים בליבותיהן של גלקסיות אחרות, הדמיה ברזולוציה גבוהה יכולה להוסיף ראיות לנוכחות של חורים שחורים סופר-מאסיביים מרכזיים. סוג זה של הדמיה יכול להיעשות ברמת הפרדה של 0.1 שנית קשת, באמצעות טלסקופ החלל האבל, או ברמה של 0.3-0.4 שנית קשת באמצעות טלסקופים ארציים באתרים גבוהים (ניתן להגיע להפרדה גבוהה יותר בתחום אינפרא אדום באמצעות אופטיקה מסתגלת). בפארסק המרכזי של גלקסיה M 32, השייכת לקבוצה המקומית, מזהים שיא חד בכמות האור הנפלטת. גם בגלקסיית אנדרומדה, M 31, ניתן לזהות עליה בריכוז האור סמוך למרכז. צפיפות הכוכבים במרכז M 32 עולה פי 100 מיליון בהשוואה לצפיפות הכוכבים בקרבת השמש. מודלים המסבירים את העלייה בכמות אור מצביעים על קיום חור שחור שמסתו כ- 3 מיליון מסות שמש. לפי ניתוח זה במרכז גלקסיה M31 שוכן חור שחור שמסתו 10 מיליון מסות שמש. עם זאת, השיא של האור במרכז הגלקסיה אינו נקודה סינגולרית של חור שחור; היא עשויה גם להעיד על קיומו של צביר כוכבים צפוף מאוד.

באדיבות teachastronomy
הפיזיקה של החורים השחורים העל-מסיביים הללו אינה שונה מהותית מהפיזיקה של החורים השחורים מאסיביים, הנוצרים באבולוציה של הכוכבים הגדולים ביותר. גודל רדיאלי של חור שחור ניתנת על ידי רדיוס שוורצשילד, RS = 2GM / c2 (עבור השמש, רדיוס שוורצשילד הוא 3 ק"מ). לכן חור שחור שמסתו 106 מסות שמש יש רדיוס 106 × 3 ק"מ וחור שחור בעל 109 מסות שמש יש רדיוס של 109 × 3 ק"מ. הקוטר של החור השחור מסיבי יותר הוא 40 יחידות אסטרונומיות, או רק 0.0002 פארסק. תארו לעצמכם את המסה של מיליארד שמשות ארוזה לתוך נפח בגודל של מערכת השמש! אנחנו יכולים להשתמש במשוואה עבור זוויות קטנות כדי להראות עד כמה קשה יהיה לזהות את קיומו של חור שחור על-מסיבי בגלקסיה סמוכה. הזווית הקטנה ביותר שניתנת להפרדה על ידי טלסקופ החלל האבל היא 0.05 שניות קשת. במרחק של D = 106 PC, בקבוצה המקומית, גודל התופעה הקטנה ביותר שניתן לזהות היא d = Da / 206,265 = 106x 0.05 / 206,265 = 0.2 pc. במרחק של אשכול בתולה, התופעה המינימלית שניתן להפריד גדולה פי 1.5, או 3 PC. אפילו עבור הגלקסיות הקרובות ביותר, אנחנו מוגבלים בהפרדה של תופעות שקוטרן אלפי פעמים רדיוס שוורצשילד. הראיות שלנו לחורים שחורים סופר-מאסיביים הן עקיפות. עלינו להסיק את קיומו של חפץ קומפקטי מהשפעתו על הכוכבים והגז המקיפים אותו – קישור להדמיה של תנועת כוכבים סביב מרכז גלקסיית שביל החלב.
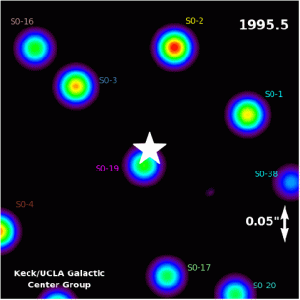
באדיבות UCLA
בדיוק כמו שניתן לפענח פשע ללא עדות מהימנה, גם במקרה של חור שחור, ניתן לזהותו מבלי "לראות" את החור השחור. בהסתמך על כל קווי הראיה העקיפים שלנו, האסטרונומים מאמינים כי אנו יכולים לומר בוודאות שחורים שחורים סופר-מאסיביים הם תכונה סטנדרטית בכל הגלקסיות הקטנות, ויתכן שאפילו בגלקסיות הקטנות ביותר. בסקר שנערך על ידי ג 'ון קורמנדי (Kormendy) ואחרים נמצאו עדויות לקיום חורים שחורים בכ- 25% מהגלקסיות הסמוכות. נראה כי מסת החור השחור העל-מאסיבי תלויה במסה של המרכיב הכדורי של גלקסיה. בגלקסיות ספירליות, המסה של הבליטה המרכזית מכתיבה את מסת החור השחור. בגלקסיות אליפטיות, כל המסה הכוכבית מכתיבה את מסת החור השחור. עבור גלקסיות מכל סוג, החור השחור הוא מסיבי, אך עדיין הוא מהווה רק חלק קטן מהמסה הכוללת של הגלקסיה, רק 0.1%. מהכוחות אפלים פועלים בלבן של גלקסיות רבות.
זה נראה מוזר לעסוק בחורים שחורים על מסיביים כאשר הראיות עבור חורים שחורים של כוכבים מסיבים חזקות אבל עדיין לא מכריעות. אך מצב החומר בגוף קומפקטי שכזה אינו יוצא דופן. נתחיל בחור שחור בעל מסת שמש אחת. אם 2 × 1030 kg מעוכים בתוך רדיוס של 3 ק"מ, הצפיפות היא 1019 km/m3 צפיפות יוצאת דופן. הצפיפות פרופורציונלית למסה חלקי רדיוס בשלישית r ∝ M/R3, ראינו שרדיוס שוורצשילד נמצא ביחס למסה. שילוב של יחסים אלה נותן התוצאה עבור הצפיפות של חור שחור הנמצא ביחס לריבוע המסה, r α M-2. במילים אחרות, חורים שחורים סופר-מאסיביים הם פחות צפופים מאשר חורים שחורים רגילים. כלומר, אם חור שחור בעל של מסת שמש אחת צפיפותו 1019 kg/m3, אז לחור שחור בעל מיליון מסות שמש יש צפיפות של kg/m3 יkg/m3 1019/(106)2 = 107 , ולחור שחור שמסתו ומיליארד מסות שמש צפיפות של kg/m3 יkg/m3 1019/(109)2 = 10. המספר האחרון שהתקבל גדול רק פי עשרה מצפיפות האוויר שאתה נושם! חורים שחורים סופר-מסיביים הם צפופים פי מאה ממים! קיימת הנחה,שהמסה מחולקת באופן שווה בתוך רדיוס שוורצ'ילד, אך אין לנו סיבה להאמין שזה נכון. עם זאת, הפיזיקה של חורים שחורים אינה אינטואיטיבית ומרתק לחשוב עליה.
Author: Chris Impey

