האם ניתן לשקול גלקסיה? למעשה, ניתן למדוד את המסה של גלקסיה באמצעות תנועתו של כוכב אחד בתוכה! בדרך דומה לדרך שבה הסתייענו בחוקי קפלר כדי למדוד את המסה של כוכבים במסלולים של מערכות בינאריות, ניתן להסתייע בחוק השלישי למדידת מסה של גלקסיה. המסה M תבוטא ביחידות מסת שמש, רדיוס המסלול a ביחידות אסטרונומיות (י.א.) וזמן המחזור P בשנים, המשוואה שהתקבלה עבור זוג במערכת בינארית היא:

P2 = a3 / (MA + MB)
נציב עתה במקום MA את מסת גלקסיה בתוך מסלול השמש, ובמקום MB את מסת השמש. MA גדול הרבה יותר מאשר MB, אנחנו יכולים להחליף סכום המסות במסת הגלקסיה בלבד MG. עבור a נבחר את מחצית הציר המרכזי של מסלול השמש סביב המרכז הגלקטי. (ניוטון הראה כי השמש מגיבה רק למסה בתוך מסלולה, ולכן חישוב זה אינו מתייחס למסת הגלקסיה שמחוץ למסלול השמש.) לבסוף, נוסיף קבועים מספריים למשוואה, ונקבל:
P2 = 4π2r3 / G MG
במסלול מעגלי, זמן המחזור מתקבל ע"י חלוקת היקף המסלול במהירות המסלולית, או P = 2πr / v. הצבת ביטוי זה במשוואת החוק השלישי של קפלר, וארגון המשוואה מחדש, נותן:
MG = rv2 / G
G הוא קבוע הכבידה העולמי, עם ערך של 10-11 × 6.67 ביחידות של Newton × m2/kg2. כעת אנו יכולים להכניס את הערכים הידועים של r ו- v, תוך הקפדה על שימוש ביחידות מטריות עבור r ויחידות km/s עבור v. מהירות המסלול של השמש היא
v = 225 km/s, או 105× 2.25 מטר/שניה. המרחק למרכז הגלקטי הוא r = 8500 PC, או 1016 × 3 × 8500 מטר. התוצאה שמסת הגלקסיה בתוך מסלול השמש היא:
MG = 2.55 × 1020 x (2.25 × 105)2 / 6.67 × 10-11 = 1.9 × 1041 kg.
מסה אחת סולארית היא 1030 × 2 ק"ג, כך שסך המסה בגלקסיה הנמצאת בתוך מסלול השמש היא:
1.9 × 1041 / 2 × 1030 ≈ 1011 solar masses
המספר העצום הזה משקף רק את החומר שבין המסלול שלנו לבין המרכז הגלקטי, ולכן ברור שהוא פחות מהמסה הכוללת של הגלקסיה שלנו.
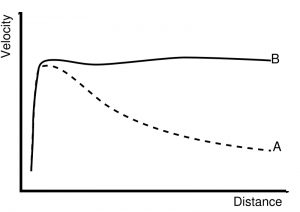
גרף A מציגה את המהירות הצפויה לו פיזור החומר היה בהתאם למסה הנראית של הגלקסיה. גרף B מציג את המדידות שבוצעו.
באדיבות וויקיפדיה
עכשיו אנו יכולים גם לראות מדוע עקומת הסיבוב של כוכבים בשביל החלב מרמזת על מסה ההולכת וגדילה באזורים החיצוניים של הגלקסיה. במשוואה הנ"ל ניתן להשתמש כדי לחשב את המסה בתוך כל מסלול מעגל בדיסקת הגלקסיה. עקומת סיבוב שטוחה פירושה שהמהירות המסלולית של כוכבים בגלקסיה אינה עולה או יורדת עם השתנות המרחק ממרכז הגלקסיה. למעשה, המהירות המסלולית נשארת כמעט קבועה. G הוא גם קבוע, ולכן אנו מסיקים כי:
MG α r
זו היא תוצאה יוצאת דופן. במקרה של מערכת השמש, המסלולים הקפלריים של כוכבי הלכת מגיבים רק למסת השמש. כאשר עיקר המסה של המערכת נמצאת במרכז המערכת, משוואת החוק השלישי של קפלר במערכת השמש מובילה ליחס v ∝ 1/πr. מהירויות מסלוליות של כוכבי הלכת הולכת וגדילה ככל שקטן מרחק הפלנטות מהשמש, כלומר עקומת הסיבוב יורדת עם הגידול במרחק. בגלקסיה שלנו, עקומת הסיבוב בגלקסיה שלנו נשארת שטוחה כאשר הרדיוס גדל. מכאן, שמסה של הגלקסיה ממשיכה לגדול גם כאשר רדיוס הגלקסיה גדל.
Author: Chris Impey

