ניתוח ספקטרום השמש, הנובע מקרינת החום של הפוטוספרה מצביע על טמפרטורה של 5700K. ניתן לראות בשמים כוכבים כחולים או אדומים יותר מהשמש – הצילומים שלהם מעידים שהם חמים או קרים יותר מהשמש. אבל עד כמה כוכבים אלה גדולים בהשוואה לשמש? חוק סטפן-בולצמן מתייחס לגודל הכוכב לטמפרטורה ולנגיהות שלו; חוק זה חל לא רק על כוכבים אלא על כל גוף הפולט קרינת חום (כולל סללים זוהרים בתנורים חשמליים, וחוטים בנורות להט). הצורה המתמטית של החוק קובעת כי הנגיהות L פרופורציונלית לשטח הפנים של הכוכב כפול החזקה הרביעית של טמפרטורת פני השטח שלו:
L = 4 π R2 σ Τ 4

באדיבות Teach Astronomy
אם הרדיוס R של הכוכב נתון במטרים והטמפרטורה בקלווין, הקבוע המספרי σ = 5.67 x 10-8 כך שהנגיהות תתקבל בוואט. (באופן לא מפתיע, σ נקרא קבוע סטפן-בולצמן.)
נגיהות הכוכב קשורה לגודל שטח הפנים שלו ולכמות האנרגיה הנפלטת בכל מטר מרובע של השטח (σ Τ 4). ניתן לשנות רק את הטמפרטורה או רק את הרדיוס של כוכב כדי לראות איזו השפעה יש להם על הנגיהות. אם הטמפרטורה של כוכב מוכפלת, כמות האנרגיה המוקרנת עולה פי 24 = 16. לכן, הכפלה של רדיוס כוכב תגדיל את הנגיהות פי 4. כוכבים חמים לא רק מקרינים אור כחול יותר מכוכבים קרים יותר (תוצאה המתקבל על פי חוק ווין) אלא גם פולטים יותר קרינה לכל יחידת שטח בכל אורך גל. נא לזכור שלאור כחול יש אנרגיה גבוהה יותר מלאור אדום. ניתן לחשוב על כך כאשר מחממים מוט ברזל, צבעו משתנה מאדום עמום (בטמפרטורות נמוכות יחסית) לצהוב לבן (בטמפרטורות גבוהות יותר).
לפניכם היישום של משוואת סטפן-בולצמן לגבי השמש. הנגיהות של השמש הוא 3.8 כפול 1026 וואט וטמפרטורת פני השטח (או הפוטוספרה) היא: 5700K . סידור מחדש של המשוואה נותן:
R = √ (L / (4 π R2 σ Τ 4)) = √ (3.8 x 1026/(4 π x 5.67 x 10-8 x 57004)) = 7X108 meter
ניתן להפעיל משוואה זאת על כל כוכב. אם יש בידיכם את נגיהות הכוכב וטמפרטורת פני השטח שלו ניתן לחשב את הרדיוס. אסטרונומים מבצעים אבחנות רבות של התפתחות כוכבים באמצעות תרשים הרצספרונג-ראסל, או דיאגרמת HR. דיאגרמה המציבה את נגיהות הכוכבים ביחס לטמפרטורות שלהם. כך שניתן להשתמש בחוק סטפן-בולצמן כדי לחשב רדיוס לכל כוכב המופיע בדיאגרמה.
מה שמשמעות החוק של סטפן-בולצמן לגבי כוכבים בעלי נגיהות וטמפרטורה שונים למדי מהשמש? סידור מחדש של המשוואה כאשר רדיוס הכוכב נמצא בצד שמאל נותן:
R ∝ √ L / T2
במשוואה זו, הסמל ∝ פירושו "פרופורציונאלי". כך ניתן להשוות את השמש לכוכבים אחרים, ובמקרה זה מתבטלים הקבועים המספריים בחוק סטפן-בולצמן. אם נסמן ב- "*" כוכב כלשהו, וב- ☉ (או מעגל עם נקודה בתוכו) את השמש, נוכל לכתוב:
R * / R☉ = √ (L * / L☉) / (T * / T☉) 2
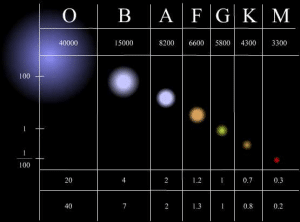
באדיבות Teach Astronomy
קיימת משפחה שלמה של כוכבים, המכונים כוכבי הסדרה הראשית, היוצרים אנרגיה על ידי היתוך של מימן להליום במרכזם. הנגיהות של הכוכבים המסיבים בסדרה הראשית גדולה פי מיליון מזו של השמש, וטמפרטורת פני השטח שלהם מגיע כדי 40,000K . לכן,
L * / L ☉ = 106
ו-
T * / T ☉ = 40,000 / 5700 = 7.
אם נציב נתונים אלה במשוואה האחרונה נקבל
R * / R ☉ = √ (106) / 49 = 20. משמעות הדבר שקיימים כוכבים הגדולים פי 20 מהשמש המתיכים מימן להליום. מאידך קיימים כוכבים בעלי מסה נמוכה מזו של השמש, שהנגיהות שלהם היא רק אלפית מזו של השמש וטמפרטורת פני השטח שלהם 2300K בלבד. אנו רואים כי
L * / L ☉ = 10-3 ו- T * / T ☉ = 2300/5700 = 0.4.
בדרך דומה נקבל R * / R☉ = √ (10-3) / 0.16 = 0.2. כלומר, ישנם כוכבים שקוטרם חמישית מקוטר השמש והם מתיכים מימן להליום.
חישובים של גודל הכוכבים מניבים גם תוצאות מפתיעות אם ניקח בחשבון שקיימים כוכבים מאותו סוג ספקטרלי (טמפרטורה) כמו השמש, אך הם בעלי נגיהות שונה בהשוואה לשמש. כוכבים בעלי אותו סוג ספקטרלי הם בעלי טמפרטורת פני השטח זהה. במקרה זה, חוק סטפן-בולצמן הופך פשוט עוד יותר את R ∝ √ L . ישנם כוכבים עם צבע זהה לשמש אך הנגיהות שלהם גדולה פי 100,000 מזו של השמש. כוכבים ענקיים אלה חייבים להיות גדולים פי (105) √= 300 מגודל השמש. ישנם כוכבים בעלי אותו צבע כמו השמש שנגיהות שלהם היא רק 1/10,000 מזו של השמש. אלו כוכבים ננסיים שחייבים להיות בעלי גודל השווה (10-4) √= 0.01 מגודל השמש. למרות שהשמש היא כוכב טיפוסי, מגוון סוגי הכוכבים עצום! בכל מקרה, חוק סטפן-בולצמן מאפשר לנו להעריך את גודלם ללא מדידה ישירה.
Author: Chris Impey

