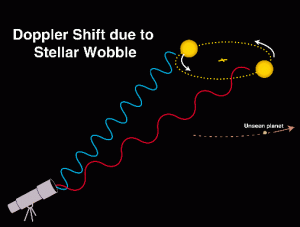
באדיבות וויקיפדיה
הכוכבים נעים, למרות שתנועתם אינה מורגשת במהלך חיי אדם, מפני שמיקום הכוכבים בשמי הלילה (או צורת קבוצות הכוכבים) אינה משתנה כמעט בפרק זמן זה. אך הספקטרוסקופיה מאפשרת לנו ללמוד על מאפיין חשוב זה של הכוכבים. אפקט דופלר מאפשר לזהות חלק מתנועת הכוכבים – המהירות הרדיאלית שלו, או תנועתו לאורך קו הראייה. אפקט דופלר מתרחש מפני שגלי האור מתקצרים אם מקור האור (הכוכב) נע לעברנו, או מתארכים אם מקור האור מתרחק מאתנו. שינוי אורך הגל בעקבות אפקט דופלר נמצא ביחס ישר למהירות הכוכב, וגודלו זעיר – שבריר ממהירות האור. יש לנהוג בזהירות כדי להבחין בהסחת דופלר כתוצאה מהשינוי בספקטרום התרמי של הכוכב, המשפיע על מדידת הטמפרטורה של שטח פניו, כפי שמתואר על ידי החוק של ויין. הסחת דופלר היא אינדיקציה לתנועה, אך לא אינדיקציה לשינוי הטמפרטורה של פני הכוכב. מאחר והסחת דופלר של כוכבים קטנה מאוד, בדרך כלל פחות 0.1%, אנחנו לא יכולים לזהות שינוי בצבע של הכוכב. במקום זאת, אנו משתמשים בתכונות ספקטראליות מובהקות כדי למדוד את השינוי.
הסחה עקבית לכחול או לאדום של כל הקווים הספקטראליים של כוכב מוכיחה שהכוכב נע לעברנו או מתרחק מאתנו. לדוגמה, אם הכוכב מתרחק ב- 0.1% ממהירות האור (או 300 ק"מ לשנייה), האור יעבור הסחה לאדום, אורך גל יגדל 0.1% בהשוואה לאור של כוכב הנמצא במנוחה ביחס אלינו. קו בליעה שנמצא בדרך כלל באורך גל 500.0 ננומטר יופיע ב- 500.5 ננומטר (ננומטר הוא מיליארדית של מטר או 10-9 מטר). אם הכוכב מתקרב אלינו ב- 0.02% ממהירות האור (או 60 ק"מ לשנייה), ההסחה לאדום תהיה 0.02% מאורך הגל הרגיל. במקרה זה, קו שנמצא בדרך כלל ב 500.0 ננומטר יוסח ל- 499.9 ננומטר. לכוכבים הקרובים יחסית לשמש יש מהירות רדיאלית של 10 עד 20 ק"מ; כמחציתם בעלי הסחה לאדום וכמחציתם מוסחים לכחול.
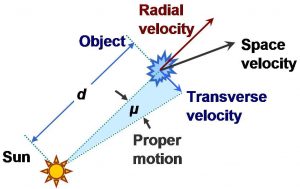
באדיבות astropedia
המרכיב השני בתנועה של כוכבים הוא המהירות המשיקית – זוהי התנועה הניצבת לקו הראייה. לא ניתן למדוד מהירות זו בדרך פשוטה כמדידת המהירות רדיאלית. כדי למדוד את מהירות משיקית, עלינו למדוד את המרחק של הכוכב ואת המהירות הזוויתית שלו על פני השמים (proper motion). מהנתונים שהוצגו לעיל, ניתן לחשב את גודל המהירות הזוויתית. אם המהירות המשיקית של הכוכב היא 20 ק"מ לשנייה, אזי הוא יעבור 20 × 3600 × 24 × 365 = 108×6.3 ק"מ בשנה. חישוב הזווית שיעבור הכוכב נעשית באמצעות הקרוב של זוויות קטנות. לפי קרוב זה הזווית שיעבר הכוכב בשנה בשניות קשת היא 206,265 (d/D), כאשר 108×6.3d= ק"מ. אם נניח שמרחק הכוכב 1 פארסק או D = 3 × 1013 ק"מ. אז הזווית היא:
1.3 × 1013 /( 3 × 1013) = 0.4 שניות קשת בשנה. גודל קטן אבל מדיד.
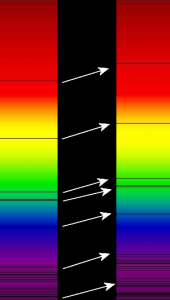
באדיבות וויקפדיה
כמובן, שמרחק של 1 פארסק הוא המרחק של הכוכב הקרוב ביותר לשמש ולכן זוהי המהירות הזוויתית הגדולה ביותר האפשרית. המהירות הזוויתית תהיה קטנה יותר עבור כוכבים איטיים או רחוקים יותר. לדוגמא: 0.04 שניות של קשת בשנה עבור כוכב במרחק 10 פארסק ו- 0.004 שניות קשת בשנה עבור כוכב במרחק 100 פארסק. לכוכבים הנמצאים בשביל החלב יש תנועות אקראיות בשלושה ממדים. המהירות הזוויתית תהיה קטנה אם הכוכב נע כמעט לחלוטין בכיוון הרדיאלי. ניתן לפצות על כך במדידה סבלנית הנמשכת למעלה משנה. בדומה למדידת מרחקים בשיטת הפרלקסה, היכולת למדוד מהירות זוויתית משתפרת באמצעות תצפיות מהחלל. הלוויין (Hipparcos (1989 – 1993 הצליח למדוד את המהירות הזוויתית של 2.5 מיליון כוכבים, והחללית גאיה, שוגרה ב- 2013, הרחיבה את המדידות לכדי 1.7 מיליארד כוכבים (נכון לאפריל 2018).
מדידות אלה של תנועת כוכבים מתבצעות לעתים קרובות יחד עם מדידת פרלקסה בענף של אסטרונומיה הנקרא אסטרומטריה. האסטרומטריה הוא תחום מחקר העוסק במדידת מיקום ותנועה של כוכבים. אם המהירויות הרדיאליות והזוויתיות ידועות, ניתן לשלבן כדי לקבוע את מהירות הכוכב בחלל (המהירות האמיתית שלו) ואת כיוון תנועתו בחלל התלת-מימדי ביחס לשמש. שני הכיוונים ניצבים זה לזה. כיוון שאחד הוא לאורך קו הראייה והשני בניצב לקו הראייה. המשפט פיתגורס המפורסם מאפשר לנו לשלב את אורכי הצדדים של משולש ישר זווית (a2 + b2 = c2). כך ניתן גם לשלב את שני מרכיבים של מהירות (va2 + vb2 = vc2, כאשר va היא המהירות הרדיאלית, vb היא מהירות משיקית, ו- vc הוא מהירות האמיתית של הכוכב בחלל). המהירות בחלל של רוב הכוכבים הקרובים לשמש היא כמה עשרות קילומטרים לשנייה וכיוון תנועתם מפוזר באופן כמעט אקראי.
Author: Chris Impey

