בשנת 1842, גילה הפיסיקאי האוסטרי כריסטיאן דופלר תופעה חשובה. כאשר מודדים גלים אורך גל שלהם תלוי במהירות של מקור הגלים ביחס לצופה. כאשר הגלים יוצאים מקור המתקרב אל הצופה הם "מצטופפים" בכיוון התנועה, כאשר המקור מתרחק מהצופה אורכי הגל "נמתחים". תארו לעצמכם אבנים מושלכות לתוך בריכה במרווחי זמן קבועים. הגלים יתפשטו במעגלים קונצנטריים ואורך הגל – המרחק בין השיאים או נקודות השפל הסמוכים – יהיה זהה בכל כיוון. אם מקור הגלים נע, האבנים פוגעות במקום אחר בכל פעם, והגלים נמצאים מחוץ למרכז כאשר הם נעים.
אם מקור גלים מתקרב אליך, המרחק בין אדוות רצופות קטן ואורך הגל מתקצר. אם המקור מתרחק מהצופה, אורך הגל מתארך. בכל כיוון אחר בין שני המקרים שנידונו, אורך הגל משתנה בצורה רציפה בין הצטופפות הגלים לבין המתיחה המרבית שלהם. מצב מיוחד נוסף מתרחש כאשר הגלים נעים ב- °90 (או גלי רוחב) ביחס לכיוון של תנועת המקור. במקרה זה אורך הגל אינו משתנה, ללא קשר למהירות מקור הגלים. שינוי אורך הגל הנובע מתנועת המקור נקרא אפקט דופלר.

באדיבות hyperphysics
אפקט דופלר חל על כל מקור של גלים. הגלים יכולים להיות אדוות על פני אגם או גלי קול הנעים באוויר. מאחר והאור הוא גם גל, מקור אור נע יגרום לאפקט דופלר. האור הנפלט מהמקור הנע לעברנו גורם להסחה לכחול. האור הנפלט ממקור המתרחק מאתנו חווה הסחה לאדום.
מידת השינוי שגורם אפקט דופלר באורך הגל ניתן על ידי הנוסחה הפשוטה
Δ λ / λ = v / c
כאשר, Δλ הוא שינוי קטן באורך גל ו- λ הוא אורך גל רגיל כאשר המקור אינו זז. שינוי אורך הגל (או אחוז) שווה למהירות המקור חלקי מהירות האור.
בזמנו של דופלר, משוואה זו פותחה עבור גלי קול. כדי לבחון את נכונותה שכרו מדענים להקת כלי נשיפה, הושיבו אותה בקרון רכבת פתוח ובקשו מהחצוצרנים לנגן רק צליל אחד, כאשר מהירות הרכבת ידועה. לאחר מכן, מדדו המדענים את השינוי בתדירות הצליל כשהרכבת התקרבה או התרחקה מרציף תחנה, הם הישוו את הצליל שהתקבל לאותו צליל כשהקרון נייח. על ידי חזרה על הניסוי עם מהירויות רכבת שונות, הם הסיקו את היחסים שהוצגו לעיל.
הנה דוגמה של אפקט דופלר באמצעות גלי קול. במקרה זה, c אינו מהירות האור אלא מהירות הקול – 330 מטר לשנייה. באיזו מהירות מכונית משטרה צריכה לנע לעברך כדי שתדירות צליל הסירנה שלה תגדל ב- 50%? הגדלת תדירות הצליל פי 1.5 פירושו להקטין את אורך הגל ב- 1.5/ 1= 0.67, או Δ λ / λ = 1/3. כדי שהדבר יקרה מכונית משטרה תצטרך לנסוע ב- 1/3 מהירות הקול, או 110 מטרים לשנייה (225 קמ"ש)! מסוכן אפילו לגבי רכב משטרתי.
אפקט דופלר עבור גלי אור הוא בדרך כלל קטן מאוד. תארו לעצמכם מטוס קרב על-קולי נע לכיווננו בלילה במהירות 1600 קמ"ש. באיזו מידה אורות הכנף שלו יעברו הסחה לכחול? נתון כי 1600 קמ"ש הם 0.44 ק"מ לשנייה, ומהירות האור הידועה 300,000 ק"מ לשנייה, אפקט דופלר היה רק היה רק x 0.44 / 300,000 = 1.5 x 10-6 או על חלק אחד במיליון. לעולם לא תראו השפעה כה קטנה.
באיזו מידה חשוב אפקט דופלר במקרה של זיהוי כוכב הלכת? כפי שניתן לראות מנקודת תצפית רחוקה, המהירות המירבית של השמש, שנגרמת על ידי צדק היא 13 מטר לשנייה – מעט מהר יותר מאשר אצן יכול לרוץ. שינוי דופלר הוא לכן:
0.013 / 300,000 = 4.3 × 10-8
או 4 חלקים מתוך 100 מיליון. לאור הנראה יש אורך גל של כ- 10-5 × 5 מטר או 500 ננומטר (ננומטר). אם הכוכב דמוי השמש היה נמשך על ידי כוכב לכת דמוי צדק, אור הכוכב יוסט מ- 500 ננומטר ל- 500.00002 ננומטר כאשר הכוכב מתרחק מאיתנו או מ- 500 ננומטר ל- 499.99998 ננומטר כשהכוכב מתקרב אלינו. המשימה של גילוי כוכבי הלכת מחוץ למערכת השמש קשה מפני שנדרשת מדידה מדויקת להפליא.
באדיבות ווידיפקיה
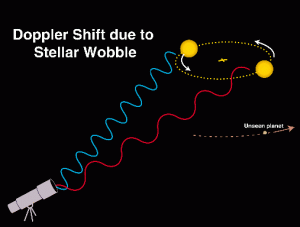
תנועה כמעט מעגלית של פלנטה יוצרת תנועה מעגלית דומה של הכוכב סביב מרכז המסה המשותף. תנועה מעגלית זו מספקת שינויים קלים בסינוס הגל,שנובע מאפקט דופלר. היינו צריכים לעשות מדידות במשך 12 שנים כדי לראות מחזור שלם של שינויים שכאלה. כדי להיות בטוחים היה עלינו להתבונן במשך למעלה מ- 12 שנים כדי לוודא כי התופעה חוזרת ונשנית.
אם נהיה ברי מזל כך שמישור מסלול הפלנטה יהיה במקביל לקו הראייה שלנו, ואז הכוכב נע ישר לעברנו או מתרחק מאתנו, בזמן שהוא מקיף את הכוכב. במצב זה אנו רואים את אפקט דופלר המלא. באופן כללי אין זה כך. נניח שהמישור של מסלול הפלנטה נוטה ב- 45 מעלות לקו הראייה. על ידי גיאומטריה פשוטה, רכיב התנועה של השמש בכיוונינו הוא cos (45º) או 0.7 פעמים קטן יותר בכל נקודה במסלול. אפקט דופלר שנצפה בו יקטן. אם כוכב לכת (מכל גודל) מקיף את כוכב מאונך לקו הראייה שלנו, לא נצפה בשום אפקט דופלר.
Author: Chris Impey

