במדע, ובמיוחד באסטרונומיה, קיימים מספרים ארוכים במיוחד לתיאור מרחקים, גילאים, טמפרטורות וצפיפות. בהחלט לא נוח לכתוב את המרחק שעובר האור בשנה – 6,000,000,000,000 ק"מ
באדיבות NASA
או את הצפיפות של המרחב בין כוכבי – 0.000000000000000000000002 גרם / סמ"ק. אסטרונומים ומדענים אחרים פיתחו שיטה יעילה לכתיבת מספרים גדולים או קטנים מאוד בשם "סימון מדעי". במערכת זו, למספר שני חלקים, המופרדים על ידי סימן הכפל. החלק משמאל לסימן הכפל הוא המקדם, והוא בדרך כלל מספר כמו 5.2 או 6.987, כאשר רק ספרה אחת נמצאת משמאל לנקודה העשרונית. חזקות של עשר המופיע מימין לסימן הכפל. לדוגמא, נכתוב את שני המספרים לעיל בסימון מדעי:
6,000,000,000,000 = 6 × 1012
0.0000000000000000000002 = 2 × 10– 24
סימון מדעי הוא הרבה יותר קומפקטי כדרך להביע מספרים גדולים וקטנים. המעריך של המספר מציין כמה מקומות יש להזיז את הנקודה העשרונית שמאלה או ימינה כדי ליצור את המספר. במילים אחרות המספר
2.51 × 105
פירושו להזיז את הנקודה העשרונית ימינה חמישה מקומות, התוצאה 251,000. מצד שני המספר,
6.8 × 10-7
פירושו להזיז את הנקודה העשרונית שבעה מקומות שמאל, כך שיתקבל המספר 0.00000068. אם יש אפס במעריך, הנקודה העשרונית אינה זזה (מה שהופך הגיוני מפני ש- 100 = 1). הנה כמה דוגמאות של מספרים שנכתבו בדרך המקובלת (בצד שמאל) וסימון מדעי (מימין):
• 0.000490372 = 4.90372 × 10-4
• 3001 = 3.001 × 103
• 0.000002 = 2 × 10-6
• 100,000,000 = 108
• 0.887 = 8.87 × 10-1
• 148,400 = 1.484 × 105
זכור כי המעריך הוא מספר הפעמים בהם יש להכפיל את המספר בעשר. לדוגמה,100 = 1, 101 = 10, 102 = 10 × 10 = 100, 103 = 10 × 10 × 10 = 1000 וכן הלאה. המספרים הנפוצים ביותר הם אלף (103), מיליון (106), מיליארד (109), ואחד טריליון (1012). כאשר ישנן יחידות, הסימון מדעי עלול להופיע בקידומת של יחידה, כגון קילומטר (103 מטר) ומילימטר (10-3 מטר). לדוגמה:
0.0000673 m = 6.73 × 10-5 m = 0.0673 mm = 67.3 µm
• 56,000 J = 5.6× 104 J = 56 kJ = 0.056 MJ
8 pc = 127 Mpc = 0.127 Gpc
• 0.0000000899 s = 8.99 × 10-8 s = 0.00899 ms = 0.899 ns
• 145 g = 1.45 × 102 g = 145,000 mg = 0.145 kg
• 51,000,000,000 W = 5.1 × 1010 W = 51 GW = 0.051 TW
כדי לעבוד עם מספרים גדולים וקטנים, צריך לדעת את הכללים של הכפלת וחלוקת בסימון מדעי. כדי להכפיל שני מספרים ביחד, יש להכפיל את המקדמים ולחבר את המעריכים. (יש להקפיד על סימן החזקה). הנה כמה דוגמאות:
(7.91 × 104) × (2 × 107) = (7.91 × 2) × 104+7 = 15.82 × 1011 = 1.582 × 1012
• (6.9 × 108) × (1.1 × 10-5) = (6.9 × 1.1) × 108+(-5) = 7.59 × 108-5 = 7.59 × 103
• (4 × 10-6) × (5.8 × 10-11) = (4 × 5.8) × 10-6+(-11) = 23.2 × 10-17 = 2.32 × 10-16
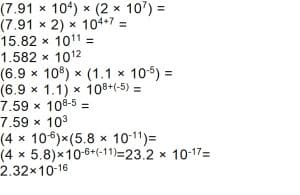
בחלוקה של שני מספרים, יש לחלק את המקדמים ולחסר את המעריכים. (שוב, יש להקפיד ולשמור על סימני החזקה כאשר אתה מחסר את המעריכים). הנה כמה דוגמאות:
(3 × 106) / (6.3 × 104) = (3 / 6.3) × 106-4 = 0.48 × 102 = 4.8 × 101 = 48
• (8.35 × 106) / (2.7 × 10-6) = (8.35 / 2.7) × 106-(-6) = 3.07 × 106+6 = 3.07 × 1012
• (7.5 × 10-8) / (9 × 10-7) = (7.5 / 9) × 10-8-7 = 0.83 × 10-15 = 8.3 × 10-14
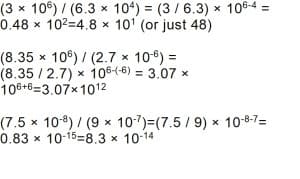
סוגריים משמשים לקבוצות פריטים ופעולות במתמטיקה. תמיד יש להשלים את הפעולות בתוך כל קבוצת סוגריים לפני המעבר אל מחוץ לסוגריים. (במילים אחרות, אין לבצע חישובים לפי הסדר משמאל לימין – אלא הסוגריים תחילה.) כאשר מופיעה בעיה המורכבת משני מספרים גדולים או יותר, העקרונות זהים. יש לקבץ את כל המקדמים להכפיל או לחלק אותם, ולקבץ את כל המעריכים ולחבר או לחסר אותם. עיין בדוגמה הבאה:
[(3.4 × 104) × (6 × 10-8)] / [(1.6 × 10-9) × (4.7 × 105)]
= [(3.4 × 6) / (1.6 × 4.7)] × 104+(-8)-(-9)-5
= (20.4 / 7.5) × 104-8+9-5
= 2.7 × 100 = 2.7
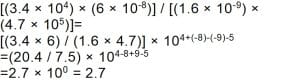
אסטרונומים משתמשים לעתים קרובות במיומנות של אמידה, כאשר הם מצרפים מספרים גדולים וקטנים כדי לקבל הערכה גסה של כמות חשובה. שמירה על מספר רב של ספרות משמעותיות אינה חשובה בחישובים אלה – האמידה אמורה להיות מדויקת רק בהתייחס לסדר הגודל. בחישובים שכאלה, המבוצעים "על גב המעטפה", לעתים קרובות שומרים אך ורק על החזקה.
Author: Chris Impey